Frequency Response Matching – Part 2

By Pat Brown

This article answers the question: If I match the “frequency response” of two components, will they sound the same?

 

In Frequency Response Matching – Part 1, I gave an overview of the concept/practice of matching the “frequency responses” of audio components to make them sound alike. I presented the impulse response IR and transfer function TF, as well as the filter types available in DSP. This article looks at the practical side of FRM.

The idea is simple – measure the “frequency response” of two components and use filters to match one of the devices to the other. The implication is that if achieved, this will make them sound the same. Can this be true?

In Part 1, I pointed out that there’s more to FRM than matching the levels of each frequency component in the response. The frequency response magnitude paints only part of the picture. There are also timing and synchronization issues between the various frequencies that ultimately determine the effect of a component on the waveforms that pass through it. FSM requires matching of both the frequency response magnitude and frequency response phase. The frequency response magnitude is blind to phase shift, polarity, and delay. A phase plot can include all three.

 

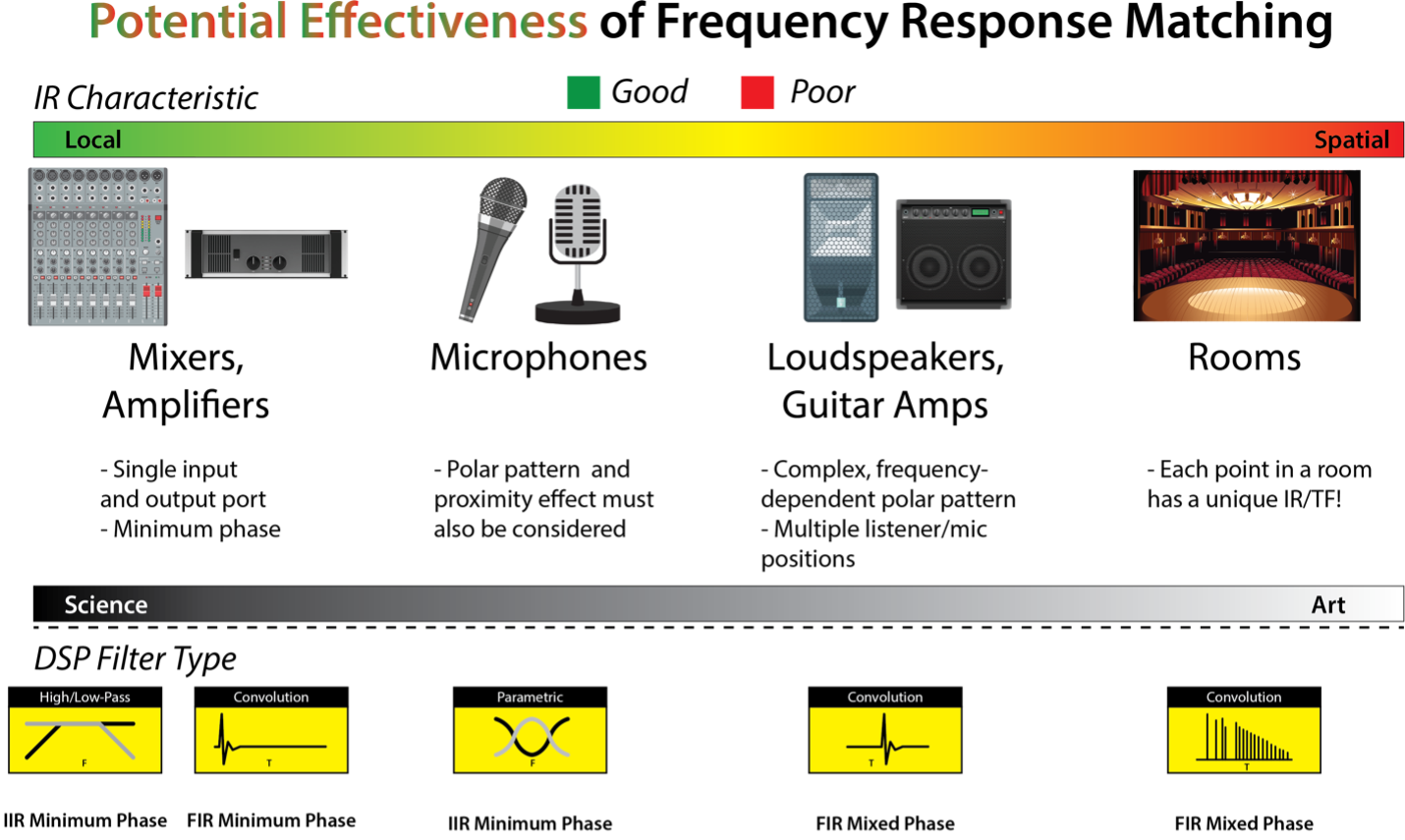
Figure 1 shows the summary graphic from Part 1 embellished for Part 2. It presents my opinion regarding the usefulness of FRM for the various parts of the signal chain. The benefits of FRM are highly correlated as to whether there is a spatial component to a device’s TF. The preferred digital filter type is also shown.

Minimum Phase
In Part 1, I also raised the issue of minimum phase. This means that the frequency response magnitude mathematically predicts the frequency response phase, and vice-versa. It also means that the component exhibits the least amount of phase shift possible, given the shape of its magnitude response. Why do we care? Min phase is a sort of Holy Grail of behaviors for an audio device. It provides reference by which a component can be evaluated. A “flat” loudspeaker (magnitude) that is minimum phase would be preferred over a “flat” loudspeaker that is non-minimum phase in applications where waveshape preservation is desired. But don’t we always desire that? Not necessarily. In audio we rarely attain these golden behaviors (and seldom need to), but we get as close as we can. One rarely finds a system response that is minimum phase in full range sound reinforcement.

Most electronic components are minimum phase. So are most microphones and single-way loudspeakers. Multi-way loudspeakers rarely are, and rooms never are. This provides a clue regarding the expectations and success of FRM. The devil is in the details, and the details are revealed by a component’s phase response.

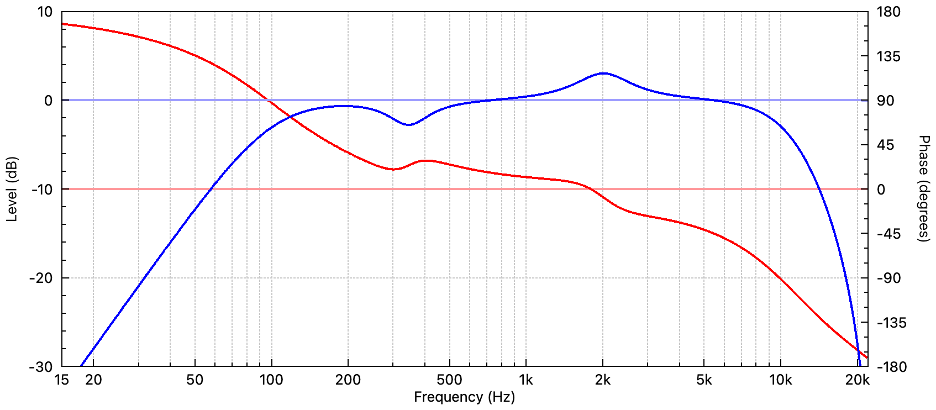
Figure 2 – The TF of this bandpass filter is minimum phase because a change in the magnitude response is accompanied by a predictable change in the phase response. The Hilbert transform of the blue plot (magnitude) produces the red plot (phase). The frequency response bumps and dips can be corrected using analog or IIR filters (digital domain). (All plots courtesy FIR Designer)

Non-Minimum Phase
If the responses to be matched are non-minimum phase then there is excess phase shift in the response, complicating the task. An FIR filter (digital domain) may still be able to match them. Figure 3 shows the response of Figure 2 with an added all pass filter and a polarity inversion. Both are non-minimum phase, making the system response non-minimum phase. Measurement programs like ARTA can import the IR and allow the measured phase response to be compared to the min phase response (determined by calculation). I produced a non-minimum phase FIR to equalize the response, yielding a near-perfect IR/TF. Note that I did not attempt to equalize the high pass and low pass behaviors. Extending the bandwidth of a component with equalization must be done with caution.

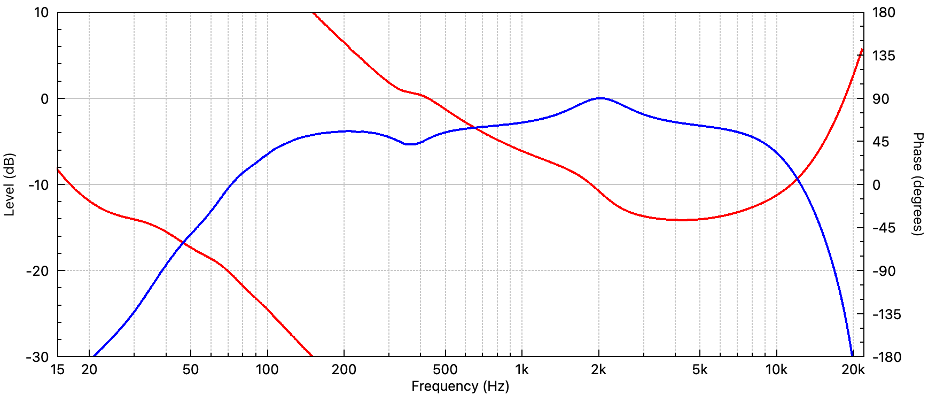Figure 3 – This component response has the following characteristics – 1. HPF (100 Hz) 2. LPF (10 kHz) 3. APF (1 kHz) 4. PEQ (2 kHz) 5. PEQ (350 Hz). It is inverted in polarity. Can this be corrected with an FIR filter?

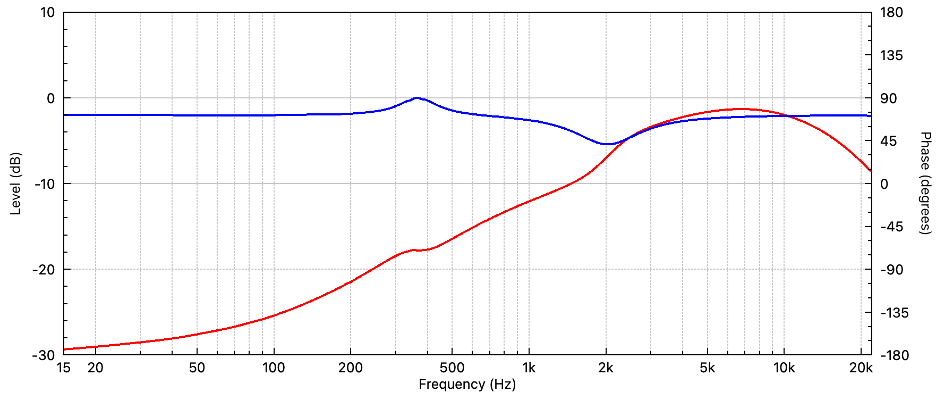
Figure 4 – This FIR correction filter has the following characteristics – 1. APF (max phase) 2. PEQ (2 kHz dip) 3. PEQ (350 Hz boost). It is inverted in polarity.

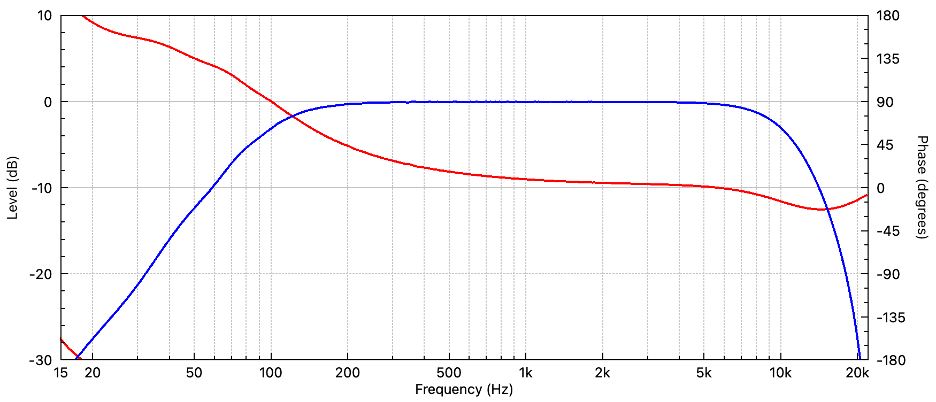
Figure 5 – Convolving the original with the correction filter yields a min phase band pass filter.

If this seems too good to be true, it is. There can be a significant penalty paid in signal delay. The FIR required to correct this response introduced over 42 ms of delay, mainly due to the max phase APF need to correct the phase response (Figure 4).

Delay is the currency of digital processing. We can have almost anything we want if we are willing to wait for it. Unfortunately, in live audio systems we can’t wait very long. Digital signal processing, especially FIR filters, provides some tools to extend the reach of FRM, but it’s not magic. There’s no free lunch and we are still faced with choosing the lesser of evils when tuning systems.

Plug-in World
Much of the excitement regarding FRM has been created by software plug-ins for mixers and DAWs. A plug-in can use convolution to impart the IR of an instrument, component, or even a room onto program material – pretty cool. These are FIR filters produced by measuring the TF of the device or room. This can be especially effective in a studio with a low noise floor and benign room response – just record the guitar “dry” and decide in post whether you want the amplifier to be a Fender Twin™, Marshall™ stack, etc. You can record a vocal with a flat reference mic and try some others using software. Pick the “keeper” and do the mix. While not as good as the real thing, software plug-ins can fool most of the people most of the time.

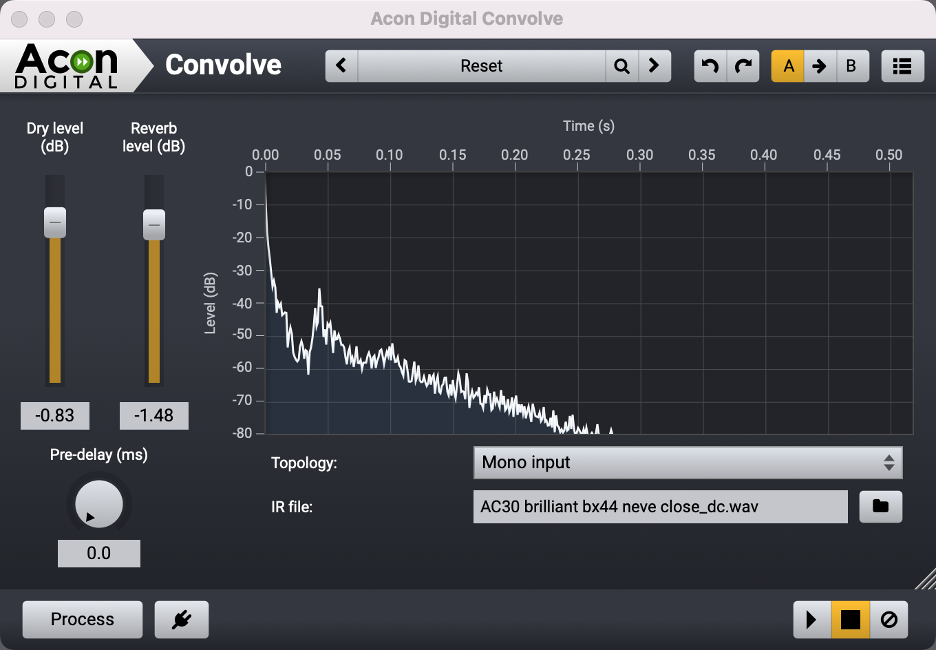
Figure 6 – A convolution plug-in used to impart the sonic signature of a Vox AC30™ amplifier onto the program material. Note: the response shown includes a room response that produces the decaying tail. An anechoic measurement must be made to impart only the amplifier’s response. (courtesy Acon Digital)

While useful in the studio, live sound is a different story. One can certainly use the same plugin on an instrument, mic, etc. but there are more variables that contribute to the resultant response. Most guitarists that I know will switch instruments if they want a different sound. A plugin isn’t going to cut it. As always, it comes down to your expectation level. FRM via a plug-in may be good enough for what it’s for, or good enough for who its for. It’s ultimately an artistic decision driven by practical implications. All live sound systems have a “latency budget” that should not be exceeded. Software plug-ins can devour it quickly. Plus, it’s a good look to have three guitars on stage instead of one.

Electronic Components
Let’s work through the signal chain, referring to Figure 1. Frequency response matching will be most effective if

1. The responses to be matched are minimum phase.
2. The device has a single input and output port.

FRM should not be necessary for mixers and amplifiers. These devices should be ruler flat and minimum phase over their audio bandwidth. If you have one that isn’t please notify the manufacturer. That said, if you are hearing differences between mixers, DIs, amplifiers, and even cables measure the TF of each and compare them.

FRM for electronic components can be accomplished with virtually any user-configurable DSP using IIR filters.

Microphones
Microphones are certainly candidates for FRM. Mics are typically minimum phase and they have a single output port. The main input “port” is on-axis, and it is at this angle that the microphone’s frequency response is typically measured. This means that the response of Mic A can be made like Mic B, at least for the axial position. It’s a perfectly valid concept to EQ one mic to sound more like another (Figure 7).

The convolution plug-ins found in some digital mixers and DAWs do this with FIR filters – at the expense of delay. Even if successful, it’s only for the angle that the IR was measured at. FRM cannot be used to match the polar responses.

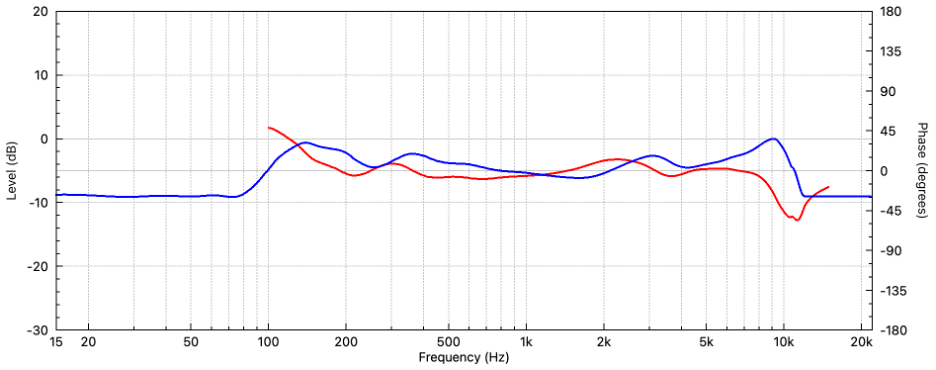
Figure 7 – This is a correction filter to flatten a popular podcast microphone. It was produced using 1/3-octave smoothing. The microphone’s phase response was ignored. This min phase filter could be deployed using an IIR filter block.

Amplifiers
Power amps are typically minimum phase with ruler flat TFs over most of their bandwidth. Under linear operating conditions there’s probably not much need for FRM. An amplifier’s response can change when it is excessively loaded and driven hard, but these non-linear response changes cannot be addressed with filters.

A Class D amplifier (the dominant class in sound reinforcement) has a passive low pass filter in its output circuit. The amplifier’s TF will be load impedance-dependent near the HF limit. This can make amplifiers sound different to people who can hear that high in frequency. If it matters, then a min phase low pass filter can be used to perform the FRM (Figure 8).

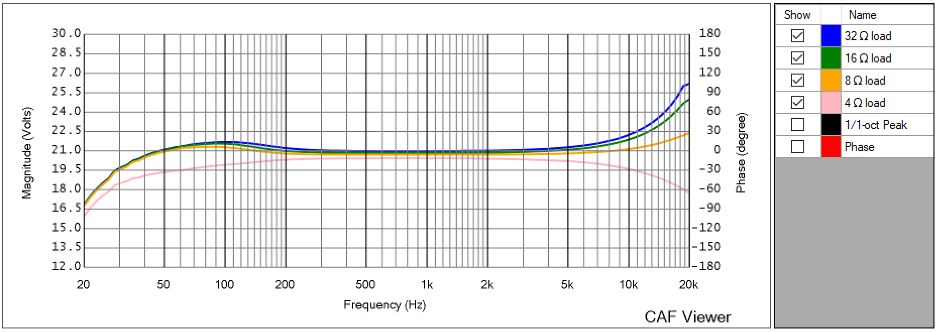
Figure 8 – The frequency response magnitude of this (and other Class D amplifiers) depends on the load impedance. Other than the 4 ohm response, it can be corrected with equalization. Such details can matter in a shoot-out.

Loudspeakers
As we work through the signal chain, FRM has proven useful so far. Things get far more complex with loudspeakers. There are many reasons why the makes and models sound different. Here are a few:

1. Most multiway loudspeakers are non-minimum phase. There is excess phase shift due to the high order crossover networks that are necessary to protect the transducers at high playback levels. Equalizing the phase response requires a maximum phase FIR filter. These can introduce significant delay, so the correction may not be worth it.
2. There are few listeners on-axis to a deployed loudspeaker, and its response is unique at all listener angles. Matching the on-axis response of two loudspeakers doesn’t match their off-axis responses.
3. Loudspeakers inherently exhibit more distortion than electronic components. The distortion increases with level. FRM cannot compensate for distortion.

So, if you want the sound of specific loudspeaker, you must buy one. That should not surprise anyone.

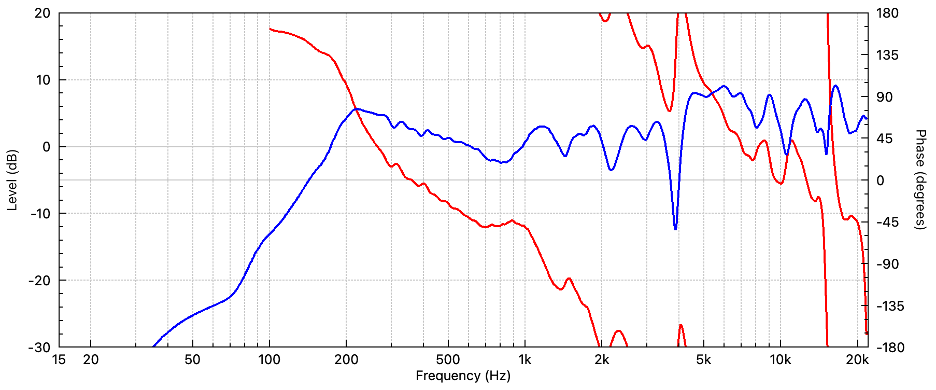
Figure 9 – The TF of a small, 2-way loudspeaker. Note that the response is non-minimum phase due to the crossover network.

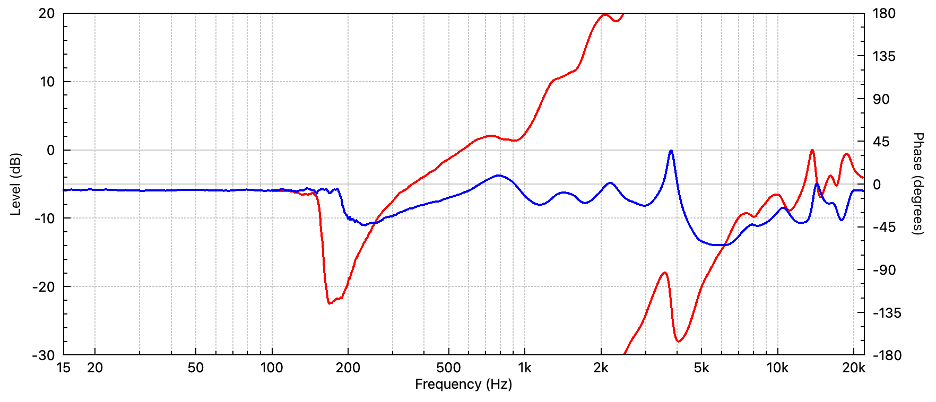
Figure 10 – This FIR corrects the TF of the loudspeaker shown in Figure 9, yielding a flat TF. It’s an 8192 tap FIR that introduces 42 ms of delay, the price paid to equalize the phase response.

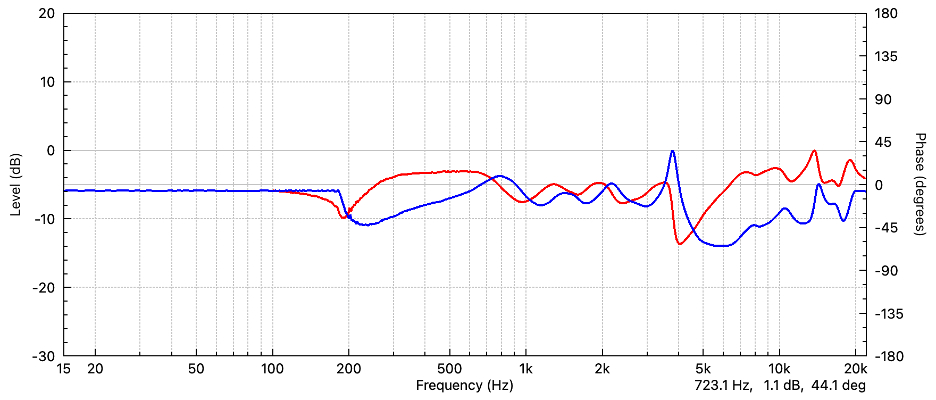
Figure 11 – This is a minimum phase FIR that smooths the magnitude response of the loudspeaker, ignoring the phase response. It is 2048 taps and introduces no processing delay. This filter could also be deployed using an IIR filter block, either manually or by importing the coefficients from a measurement software.

Rooms
One of the hottest topics in audiophile circles is “room modeling.” Electronic room correction is FRM on steroids. It seems plausible because these systems use the measured room impulse response RIR to produce the filter used for convolution. I’ll say up front that if you have done this and you like it then keep doing it. Here are some things to remember.

1. The RIR of a room is unique at every listener position within the space. Even if you “correct” it at one point, you can’t get both of your ears inside that point.
2. The RIR of a room and its TF are extraordinarily complicated. I’d say “complex” but we’ve already used that term to describe frequency response data. An FIR that “fixes” the response at a point must also be extraordinarily complicated. This means a lot of taps, and a lot of processing delay. That’s a problem in a live sound system. The more “right” the correction filter is for one point, the more “wrong” it may be for another.

Regarding FRM for room correction, it’s usually better to simplify the FIR using complex smoothing. “Perfect at a point” may look good, but it may not sound good overall. It’s also most effective when used to impart the sound of a “live” room onto a dead one, but not a live room on a live one. FRM may be able to make my heavily upholstered living room sound somewhat like Carnegie Hall, but it can’t make a high school gym sound like Carnegie Hall.

If one can make a bad room sound like a good room using FRM, then why build a good room?

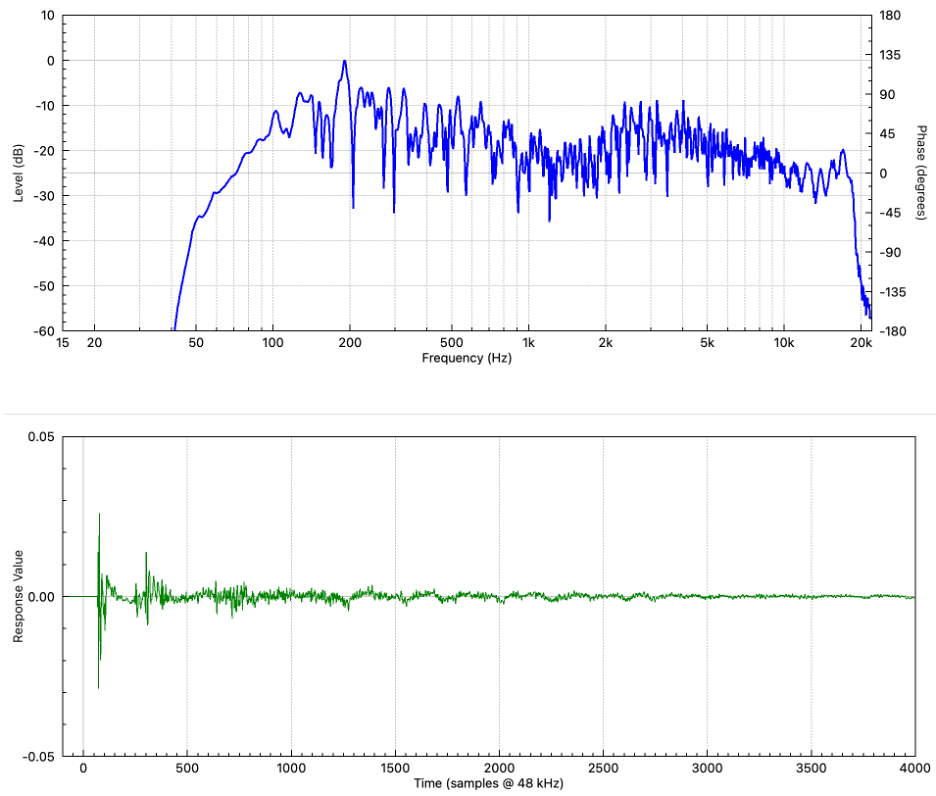
Figure 12 – This is the frequency response magnitude of a small room (top) and its IR (bottom). As I said in the text, it’s complicated. The phase response (not shown) is beyond complicated. While equalizing it is possible, it is not practical without some gross smoothing. In the real world some of the response characteristics should be ignored, such as the comb filter that begins just above 100 Hz.

Conclusion
As with most problem-solving processes or products, FRM can provide some benefits. It will disappoint if you don’t limit its scope and tamp down your expectation level. It’s mandatory for conducting meaningful comparisons of mixers and amplifiers. It’s useful for increasing the versatility of your microphones. It’s interesting when used on loudspeakers, and it’s pointless when used in large rooms. The system tuning process should involve human intelligence, compromise, and careful listening. As the IR/TF increases in detail (moving left-to-right in Figure 1) the effectiveness of FRM diminishes.

The greatest benefit of FRM is that to use it properly one must be able to make meaningful TF measurements and understand what they mean. Learning that is time well spent and a life-long process. It will reveal many ways to make your system sound better, and FRM will be one of the tools in your tool bag.  pb