Using All Pass Filters to Improve Directivity Response

By Charlie Hughes

In this article, Charlie will how all pass filters can be used to improve directivity response of a loudspeaker.

All pass filters are perhaps one of the most overlooked and poorly understood tools for the general audio practitioner. John Murray has written about their use to yield more linear phase response through the majority of a loudspeakers pass band. Their application can also be used to optimize the directivity and magnitude response of a loudspeaker system. Perhaps we should first look at just exactly what an all pass filter is.

We are all familiar (or at least should be) with a low pass and high pass filter. As their name implies they pass one part of the audio spectrum while attenuating the others. They are the basis for loudspeaker crossovers. As with any analog filter there is phase shift associated with the change in output magnitude of these filters. Examples of these are shown in Figure 1 as fourth order Linkwitz- Riley filters. If we were to add the output of these filters back together, essentially combining them with a unity gain mixer, we would get the response in Figure 2. Here we see that the magnitude response is perfectly flat; it passes all portions of the audio spectrum, thus the name all pass. However, the phase response is not flat. There is phase shift associated with this all pass behavior. This phase shift is due to the contributions of the low pass and high pass filters that were combined (mixed).

There are, of course, other ways to construct all pass filters. They can be defined mathematically, just as low pass and high pass filters can be. They can be of different orders (i.e. 1st, 2nd, 3rd, etc.) and have specific alignments (Butterworth, Bessel, Linkwitz-Riley, etc.). These alignments are not defined by the shape of the magnitude response at the corner frequency of the all pass, as we typically think of low pass and high pass filters, but by the shape of their phase response at the corner frequency. Low pass and high pass filter alignments can also be defined this way.

One difference to remember about all pass filters is that for each order there is 180° of total phase shift. Low pass and high pass filters have only 90° of total phase shift for each order. The importance of this distinction will become clear later.

Now that we have a basic understanding of an all pass filter, let’s see how one can be put to good use. Suppose that we have a two-way loudspeaker system comprised of a high frequency horn and dual 12 inch woofers as illustrated in Figure 3. The horn is located at the top of the baffle. One woofer is directly below the horn. The second woofer is directly below the first. This is a fairly typically configuration. To keep things simple we will model these components as point sources. This will make it easier to see anomalies in the directivity response of the system when the individual sources are combined. The horizontal symmetry of our example loudspeaker assures us that nothing spectacular will occur in the horizontal plane. Having the sound sources displaced vertically will yield some interesting behavior.

Since all of the good stuff will happen in the vertical plane we will be looking primarily at vertical directivity maps and a few polar plots. The nice thing about a directivity map is that it allows us to look at the relative level of different radiation angles at all frequencies at the same time, whereas polar plots only allow us to see the relative level of different radiation angles at a single frequency. Ideally we should see the same level at all frequencies and at all angles since we are using point sources (which have no inherent directivity). This will not be the case due to our vertically spaced sources.

Incidentally, all of the modeling was performed by and most of the graphs generated with the new SpeakerLab/GLL software from AFMG. It allows for some very nice investigation and optimization work to be carried out and displayed.

We have ideal text book sources so we will use fourth order Linkwitz-Riley low pass and high pass filters with a corner frequency of 1 kHz for our crossover. The on-axis summation of the sources in the far field with these filters is shown in Figure 4. This is exactly what we would expect. The low frequency level is +6 dB compared to the high frequency with a smooth transition in the crossover region. This level change is because of the two woofers compared to the one horn (the point sources we are using each have identical output). We also notice 360° total phase shift due to the fourth order filters. We get 90° of phase shift for each filter order.

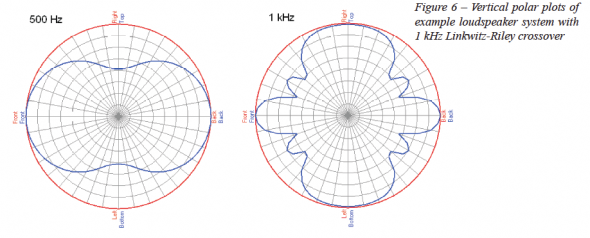
If we look at the off-axis response shown in Figure 5 we see that things are not quite so well behaved. There is considerable cancellation off-axis from 500 Hz up through the crossover region. The directivity map has frequency plotted on one axis and the vertical radiation angle on the other axis. The output level is shown both as color variation and as elevation above the frequency-radiation angle plane. All of the off-axis response data are normalized to the on-axis response. A slice through this surface at a given frequency will yield the polar response at that frequency. Similarly, a slice through any radiation angle will yield the frequency response at that angle relative to the on-axis response. For reference, polar plots at 500 Hz and 1 kHz are shown in Figure 6. Notice the deep nulls at +90° and -90° (straight up and down) in the 500 Hz polar and the same depressions in the directivity map (-20 dB green region). Also, at 1 kHz the level drops quickly at off-axis angles, increases a bit, drops again and then increases back to full level.

This is can be seen in the rippling of the directivity map. Compare this to the 1 kHz polar plot.

The cause of this destructive (cancellation) and constructive (addition) interference is that multiple sources in different locations are radiating in the same frequency region. At crossover (1 kHz) all three devices are active. The largest separation of sources is between the horn and the bottom woofer. This distance is 26 inches. This is almost exactly two wavelengths at 1 kHz. The distance between the horn and the top woofer is 13 inches, as is the distance between the two woofers. This is almost exactly one wavelength at 1 kHz. This is why there is such good summation above and below (+90° and -90°) the loudspeaker. The spacing of 13 inches between the woofers is the cause of the decrease in output above and below the loudspeaker at 500 Hz. This distance is almost exactly one-half wavelength at this frequency.

To minimize these directivity problems we need to minimize the interference. This means attenuating a source so that only one is active within a given frequency region. We can do this with the woofers by placing another low pass filter on the bottom woofer (in addition to the existing 1 kHz low pass filter used for the crossover). We’ll use a second order Butterworth low pass filter at 300 Hz to roll-off the higher frequency output of the bottom woofer. The effects of this on the vertical directivity are shown in Figure 7. The two off-axis cancellations (depressions) around 1 kHz are due to the crossover in this region between the top woofer and horn. The only way to eliminate these cancellations is to eliminate the spacing between the top woofer and horn. That is to say they would have to occupy to the same point in space, which is clearly not possible. Arranging them coaxially would not eliminate the cancellations, but it would change the angles at which they occur. We also see something very peculiar. In the 250 – 500 Hz region the directivity map is not symmetrical. There is a large region of cancellation above the loudspeaker. This is also shown in the polar plots of Figure 8. Notice the output is greater below the loudspeaker than it is on-axis.

Some readers may be thinking “No big deal, I want more output directed down towards the audience from flown loudspeakers anyway.” This is true, which is why flown or elevated loudspeakers are usually tilted downward and aimed at the audience. This “downward lobe” remains pointing along the vertical axis of the enclosure. When tilted down, this axis is usually pointing towards the stage area. Starting to see the problem.

How many line array cabinets are on the market with dual woofers or midrange drivers placed on opposites sides of the enclosure? These same directivity problems will also plague these line array cabinets but since the drivers are offset horizontally they will occur in the horizontal plane, not the vertical. I certainly don’t want to try to cover an audience area with a loudspeaker system that suffers from horizontally asymmetry over only a portion of its pass band.

This asymmetry of the directivity response is not caused by one of the woofers having more output than the other. The bottom woofer is the one that has been attenuated and the main lobe is pointed down, not up. This lobe and its asymmetry are caused by the phase shift introduced by the additional low pass filter we put on the bottom woofer. The bottom woofer now has a different, and non-complementary, phase response compared to the top woofer and the horn. To correct this all three components need to have complementary phase response.

We need to add phase shift to the top woofer and horn without altering their magnitude response. This is when we grab an all pass filter. Our 300 Hz low pass filter is second order yielding 180° of additional phase shift. To match this we need a first order all pass filter for the top woofer and the horn. When we put these filters in we get the results shown in Figure 9. The vertical directivity is once again symmetrical. The off-axis cancellations have been greatly improved when compared to Figure 5 and Figure 7.

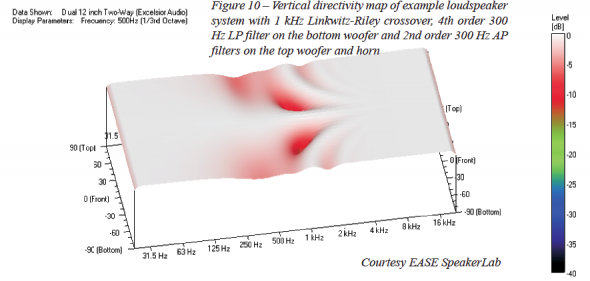
This can be further improved by using a higher order low pass filter on the bottom woofer to more rapidly attenuate its higher frequency output. We will change from the second order Butterworth to a fourth order Butterworth filter. We must also change the all pass filters on the top woofer and horn from first order to second order Butterworth. Once we use an all pass filter greater than first order we must be sure to match its alignment, or Q, to that of the low pass filter so the phase response of the low pass and all pass filters are identical. These changes give us the results in Figure 10.

The on-axis magnitude response for these final filter parameters is shown in Figure 11. Compared to Figure 4 there are only two differences. The transition from +6 to 0 dB output occurs in the 250 – 630 Hz region instead of the 630 Hz – 2 kHz region. The other is that there is one additional phase rotation in the transfer function of the loudspeaker system. While this latter difference is not ideal, it is certainly a small price to pay for the improvement in directivity response from that of Figure 5 to Figure 10.

I hope this has helped to illustrate one application of all pass filters being used effectively to improve the directivity response of multi-driver loudspeaker system.ch