Loudspeaker Maximums Part 2 – Peak SPL
Finding the Maximum Linear Peak Sound Pressure Level
In the first part of this two-part series, I described how to determine a loudspeaker’s maximum continuous input voltage (MIV) regarding heat. The MIV is the maximum RMS input voltage before the onset of power compression. When the MIV is applied to a loudspeaker, the maximum linear continuous sound pressure level (SPL) is produced. In Part 2 I’ll examine the second “loudspeaker maximum” of interest – the peak SPL.
There are two standards that describe in detail how to measure the maximum continuous and maximum peak SPL of a loudspeaker. They are
ANSI/CTA-2034 – Section 8 – On-Axis Usable Sound Pressure Level
AES75 – Measuring Loudspeaker Maximum Linear Levels Using Noise
From the CTA-2034 link you can see that it is a standard for the measurement and rating of in-home loudspeakers. This is important. The consumer audio industry has been plagued by poor rating practices that produce unrealistically high numbers for half a century. Remember “peak” power? The Consumer Technology Association should be commended for cleaning up the mess.
The CTA-2034 methods can also be used on professional loudspeakers. The instruments won’t know the difference. In CTA-2034 continuous and peak SPL are found using separate tests and completely different signal types.
AES75 measures the continuous and peak SPL in a single session using M-Noise. M-Noise claims to emulate music with regard to its crest factor, and therefore its meaningful RMS and peak levels.
If the two standards were in reasonable agreement, there would be no need for further discussion. They are not, which is why I’ve done this investigation.
Discussions on this topic are usually theoretical and philosophical, often without support from measured data. As part of this investigation, I measured five (5) loudspeakers using both standards. These include two (2) passive loudspeakers and three (3) internally powered/processed loudspeakers. The amplifier used to test the passive loudspeakers complies with the AES75 standard. For comparison, I measured both the maximum continuous SPL and the maximum peak SPL of each loudspeaker. The data are included in the appendix for those who wish to scrutinize, theorize, criticize, ostracize, etc.
Spoiler Alert
I spent a great deal of time making this article as short as possible, but it is still long. For that reason I have summarized it up front for those not interested in the details.
The results show reasonable correlation between the standards regarding the maximum continuous SPL. This is not surprising since the methods are very similar, the major difference being the noise type. So long as the bandwidth limits are considered, there are multiple noise types that can drive a loudspeaker to its thermal limit. I presented those in Part 1 of this series.
There are significant differences reported by these standards regarding the maximum linear peak SPL. The values are much higher using the AES75 method. As with the continuous SPL rating, they should at least be in approximate agreement.
Here are some “take-aways” from the investigation.
1. The standards are in close agreement on the maximum continuous SPL of a loudspeaker.
2. The standards are not in agreement on the maximum linear peak SPL of a loudspeaker.
3. Both standards claim to produce “real world” peak ratings that can be used for sound system design and marketing purposes.
The results of the testing are presented in Figure 1. All graphics can be clicked to enlarge.
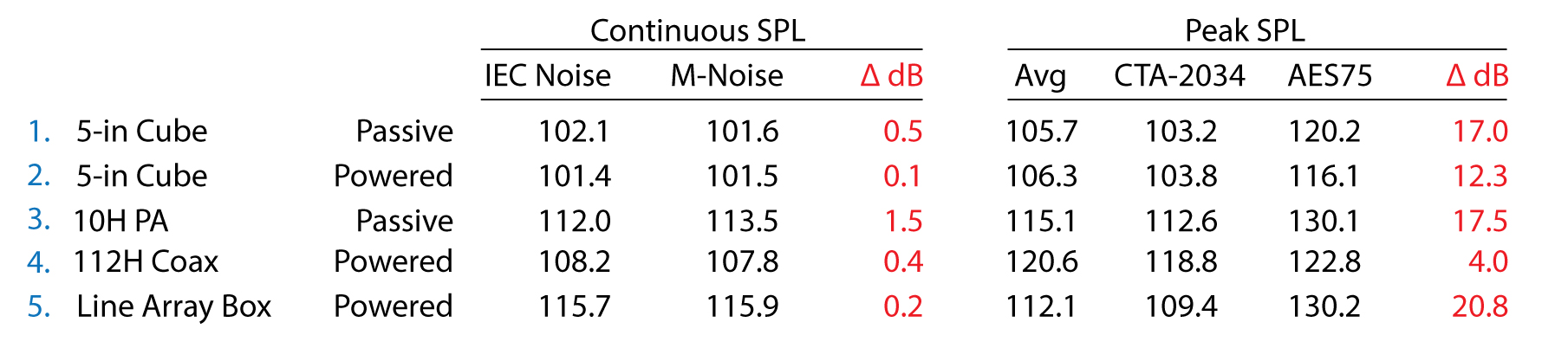
Figure 1 – The test results for each loudspeaker. The grey bars show the maximum continuous SPL. The colored bars show the maximum peak SPL. Two are based on CTA-2034 (blue, green) and one on AES75 (red).
Interpreting Figure 1
The grey bars are in reasonable agreement, as they should be. They do not agree exactly, because nothing in audio or acoustics ever does. In all cases the difference is less than 2 dB. From that I conclude that either standard can be reliably used to determine a loudspeaker’s maximum continuous SPL and MIV . Both can be used to determine the MIV used in a GLL or CLF data file. There is no reason for further discussion regarding this metric.
The colored bars should also be in reasonable agreement. They are not. AES75 produces a maximum linear peak SPL that is much higher than CTA-2034 for all of the loudspeakers.
It is important to note that both standards accurately measure the signal peak of an audio waveform. Where they differ is in their definition of a meaningful test signal for measuring the peak SPL.
The Bird’s Eye View
CTA-2034 uses a conservative approach. It considers the maximum peak SPL to be frequency-dependent and it measures it that way using wavelets. It places harmonic distortion limits on the measured signal and it does not let one frequency band dominate the results. The measured frequencies are limited to the range for which harmonic distortion is audible, relevant, and can be accurately measured.
In AES75 the peak SPL is produced by short pulses embedded in a noise waveform. The peaks exceed the RMS level of the noise by about 18 dB. Passive loudspeakers must be measured using a massive amplifier that can pass these pulses. The peak measurement is made using a Class 1 sound level meter set on “peak” mode to produce a one number rating. The peaks are not analyzed for harmonic distortion.
The remainder of this article will show why two standards that claim to produce the same specification produce very different maximum peak SPL ratings for the same loudspeakers.
Peak SPL Measurements
The MIV for the maximum continuous SPL is dependent on the spectrum of a continuous shaped noise signal, which is well-defined in both standards. The maximum peak SPL is dependent on the amplitude of an audio event. In CTA-2034 the peak testing is a separate procedure from the continuous SPL test. In AES75 pulses are embedded in the noise signal and the peak SPL is measured simultaneously with the continuous SPL.
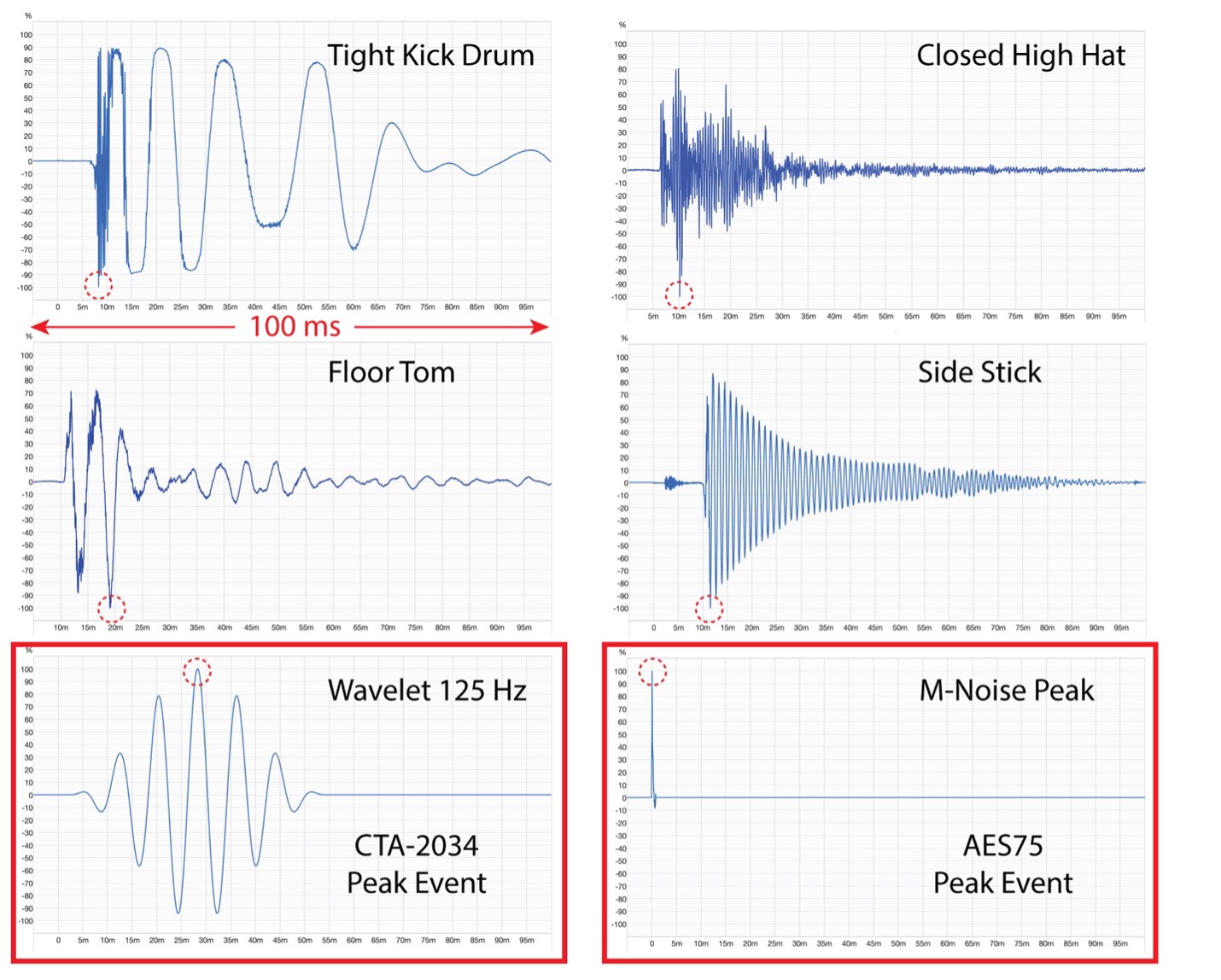
For peak testing, the waveform type is crucial. It must be meaningful regarding the use of the loudspeaker. An examination of speech and music waveforms reveals that the events of short duration are plosives in speech and percussive events in music (Figure 2). I searched an online database of sound bites to find the shortest musical events. All were percussive sounds with duration of less than 100 ms. This matters because both standards claim to emulate musical program.
In addition to the music waveforms Figure 2 also shows the waveform used by each standard to determine the maximum linear peak SPL. They are very different, and that’s important.
Figure 2 – A comparison of music transients. The plot duration is 100 ms. The red circles show the peak voltage. The heavy red boxes show the waveform and the peak event used by CTA-2034 and AES75.
Wavelet Analysis
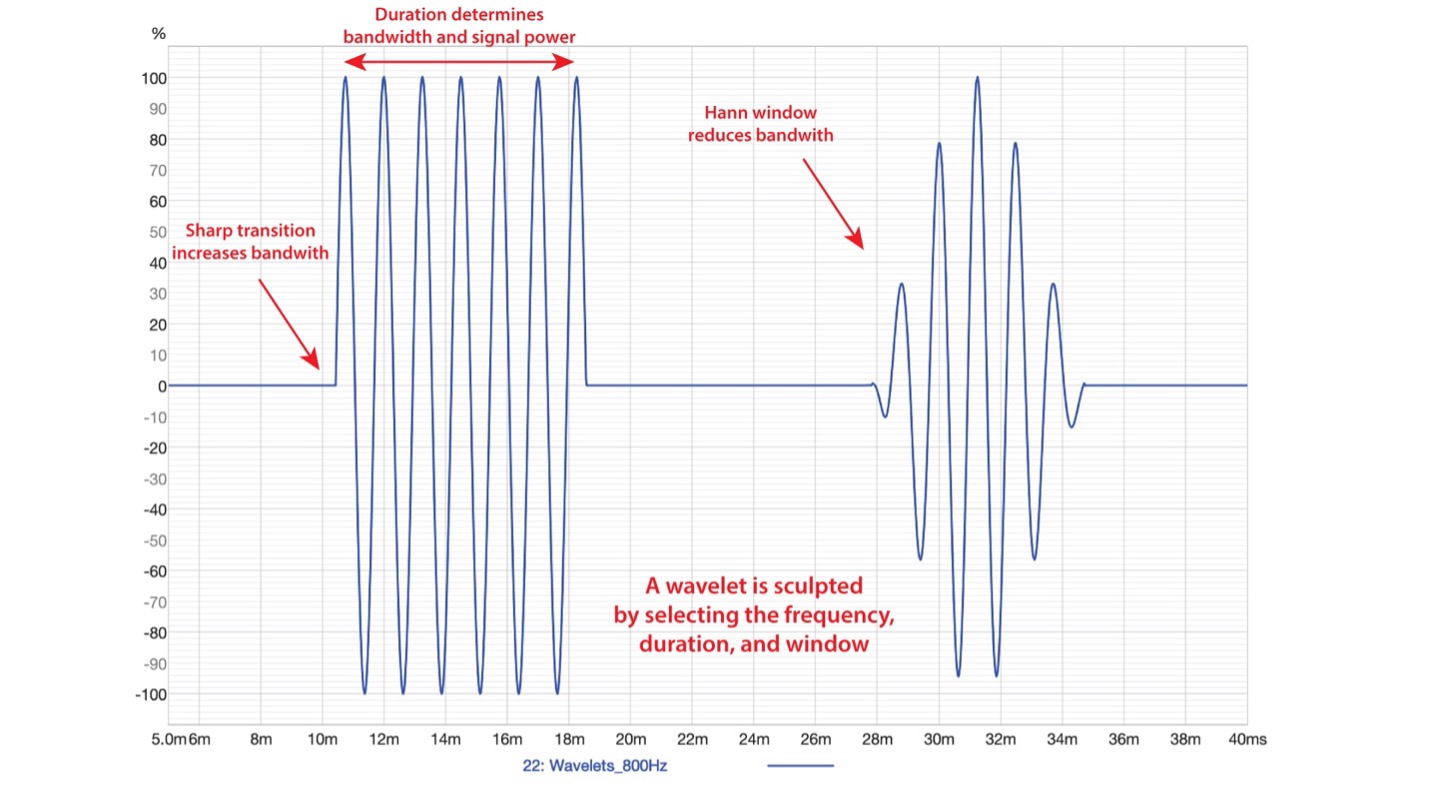
A wavelet is a short signal burst, much like the transients produced by percussive instruments and speech plosives. Figure 2 showed the time response of a wavelet compared with some common musical sounds. D.B. Keele, Jr., (audio legend and inventor of the constant-directivity horn) formalized the use of wavelets for amplifier and loudspeaker testing decades ago. Wavelets can be produced by several current software’s, including the freeware Room EQ Wizard (REW) (www.roomeqwizard.com) used in this investigation. The wavelets used by CTA-2034 are 6.5 cycles in length with a Hann window envelope (Figure 3). The base signal is a sine wave of specified frequency. The wavelet’s duration determines its spectral content (bandwidth in the frequency domain). A 6.5 cycle wavelet spans about 1/3-octave (Figure 4). Windowing the wavelet further narrows its bandwidth. A wavelet can be produced at any frequency and bandwidth by changing its frequency, length, and windowing.
Figure 3 – A sine wave burst (left) and the 6.5 cycle windowed wavelet (right) used for the CTA-2034 peak SPL test.
ANSI/CTA-2034 Overview
The Consumer Electronics Association has established several standards for loudspeaker specifications. These standards are also suitable for testing professional loudspeakers. CTA-2034 is the full-range version of ANSI/CTA-2010 – a test used to find the maximum SPL from a subwoofer. Both tests are based on applying wavelets to the system-under-test (SUT) and measuring the resultant peak SPL and harmonic distortion.
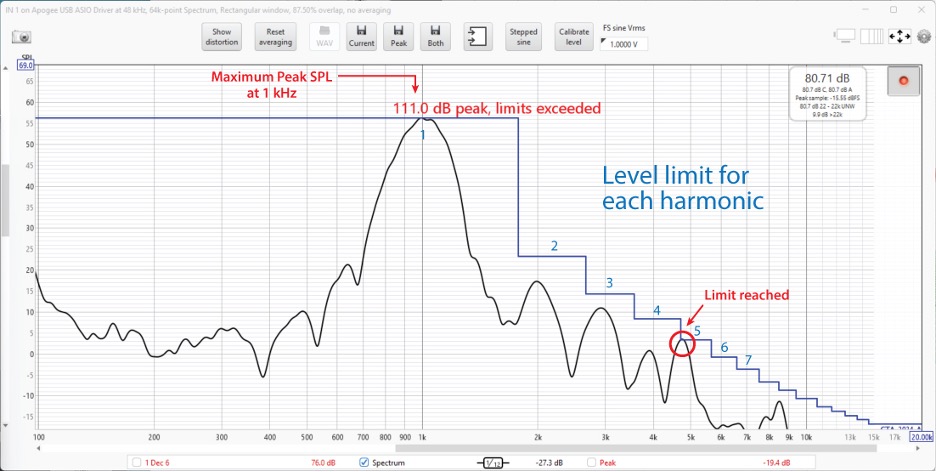
Wavelet testing can be done in the time domain with the aid of an oscilloscope. The wavelet can be inspected visually for distortion. I did it like this for years. The CTA standard further refines this test by also analyzing the wavelet in the frequency domain. The acceptable harmonic distortion limits are defined by the standard and are observed with the assistance of a stair-step guide on the display of the spectrum analyzer (Figure 4). Shown is a 1 kHz wavelet, its harmonics, and the harmonic distortion limits.
The maximum linear peak SPL is frequency dependent. The test is performed at 1/3-octave centers (18 wavelets in all) and the results plotted for further processing (Figure 5). The highest frequency wavelet is 5 kHz because the harmonic distortion products of higher frequencies fall outside of the audible spectrum.
The individual wavelet peak SPLs can be presented on a plot or in a table. A broadband, single number rating can be produced by averaging the 1/3-octave values. CTA-2034 adds an additional computational step described in the next section.
Figure 4 – A suitable wavelet must have enough cycles to establish its frequency, and steep enough “skirts” to allow the harmonic distortion to be measured. (the plot is from REW).
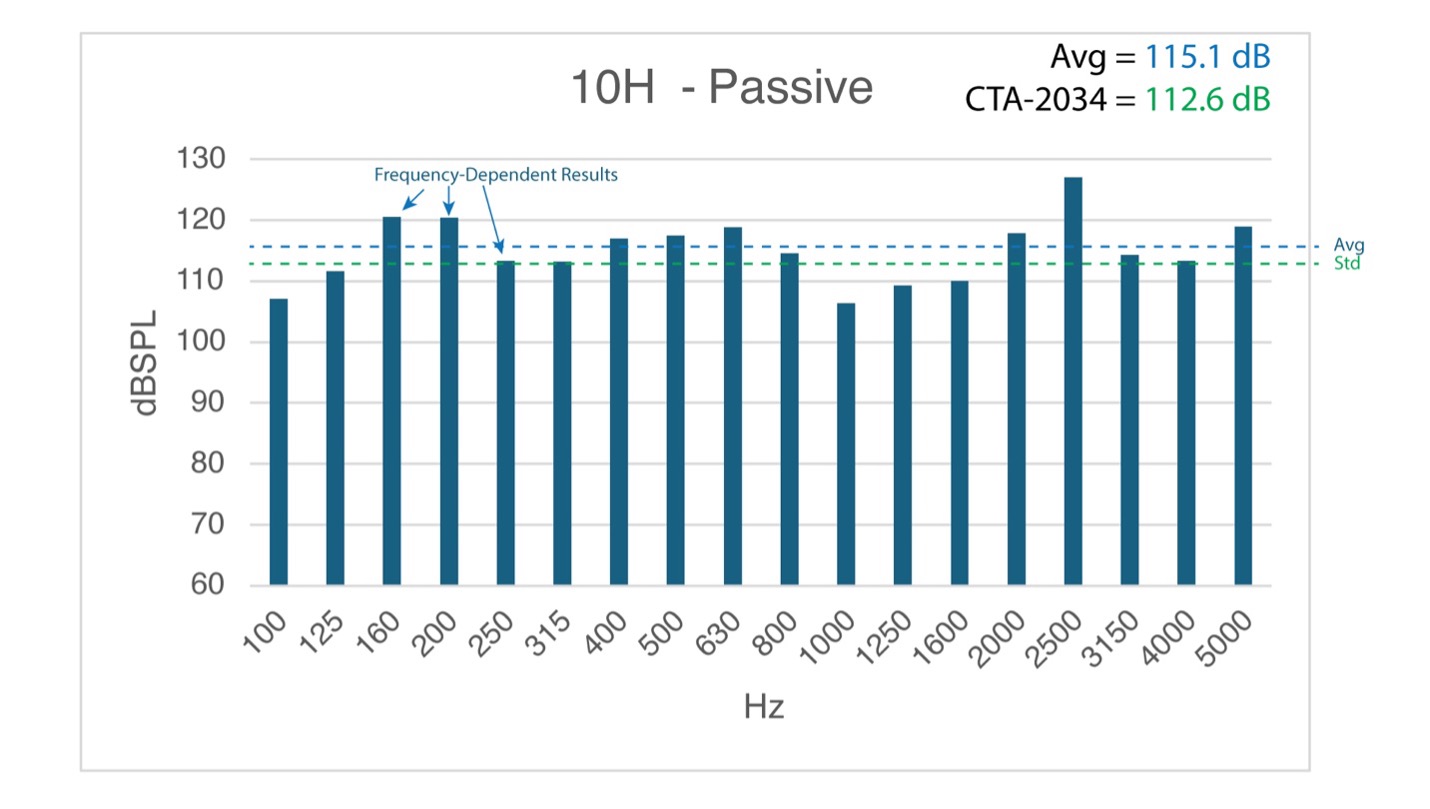
Figure 5 – The results of wavelet testing at 1/3-octave centers. I’ve shown the frequency-specific values, the average, and the CTA-2034 standard rating.
Further Post-processing
CTA-2034 looks at the wavelet response from 100 – 5000 Hz. To refine it to a single, broadband number the following steps are performed.
1. Apply weighting as per the CTA-2034 noise spectrum. This reduces the level with increasing frequency.
2. Taking the average
3. Reduce the levels exceeding the average by more than 2 dB to the average value plus 2 dB
4. Convert all values to pressure-squared
5. Calculate the sum
6. Convert back to SPL
7. Subtract 14 dB
The result is the maximum broadband peak SPL, expressed as a single number. I’ve shown this metric, along with the simple average in Figure 1 (blue and green bars, respectively).
AES75 Maximum Linear Peak Level
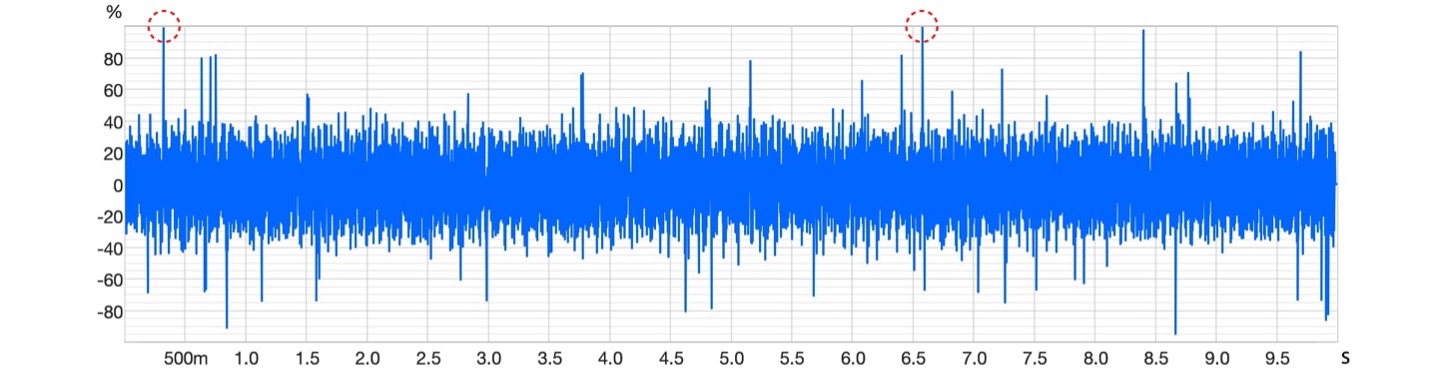
AES75 determines the maximum linear peak SPL using a weighted pink noise signal with embedded pulses (M-Noise). The time domain display in Figure 5 shows the embedded pulses. AES75 presents the maximum linear peak SPL as a single number that is frequency blind. The nature of the embedded pulses is not described by the standard, but time and frequency analysis reveals that they are very short.
Figure 5 – A ten second span of M-Noise. I’ve circled two peaks that will produce the maximum peak SPL.
Finding the Top
A major difference between the standards is how to determine when the maximum linear peak SPL has been reached. The wavelet used by CTA-2034 can be analyzed for distortion. CTA-2034 “calls the top” when a specified percentage of harmonic distortion has been reached (Figure 6).
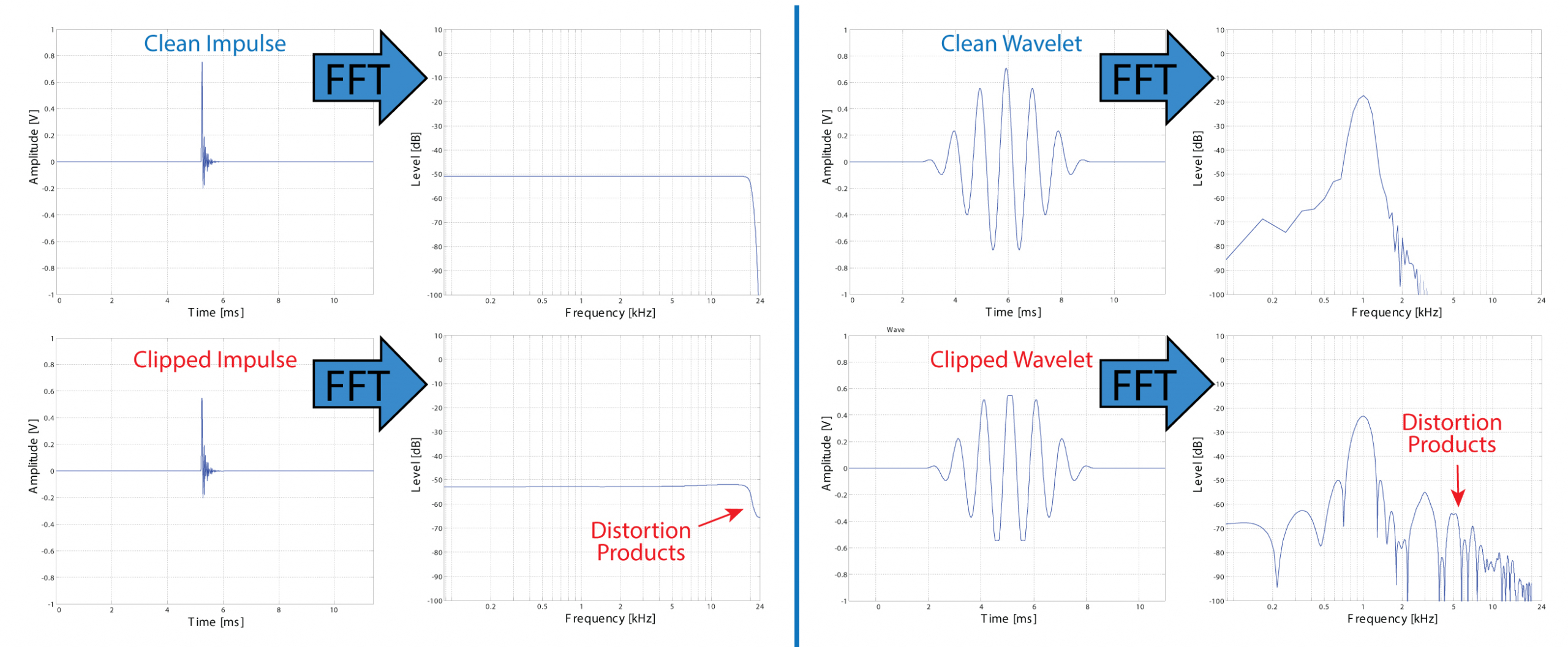
AES75 measures the peak SPL when the thermal limit of the loudspeaker has been reached. There is no analysis of the peak event, and it is likely severely clipped by any amplifier other than the massive one specified by the standard. The distortion products from a clipped impulse fall outside the analysis bandwidth. That are inaudible because a clipped impulse is still an impulse. Contrast this with the wave deformation that occurs in a wavelet test.
The coherence trace of SpeakerMeasure might catch that if the distortion products were within the analysis bandwidth (Figure 6) but it failed to do so in my testing. The use of coherence to establish a loudspeaker rating is problematic, because the coherence trace can reveal that something is wrong, but not what is wrong.
Figure 6 – The distortion products for a clipped impulse (left) are largely above the audible spectrum. A clipped wavelet (right) can be analyzed for harmonic distortion.
Let’s Listen!
If you find this confusing you are not alone. I’ve prepared a demonstration. We’re in the audio business, so let’s make some audio.
To better understand the difference between the standards, I have produced some listening tracks. Start with your playback volume low and then adjust to a comfortable listening level.
Below is a 10 s span of M-Noise. Listen carefully for the embedded pulses. These barely audible events produce the maximum linear peak SPL in AES75.
Wave 1 – M-Noise excerpt
Since the exact details of M-Noise are proprietary, I reverse-engineered it to produce a track that emphasizes the peak events by reducing the noise to a lower level. The pulses are band limited (500 Hz – 20 kHz). I did this because below 500 Hz the embedded peak events don’t exceed the peaks found in the base M-Noise signal. I mixed in some low level noise because without it some wave players won’t play the pulses due to their short duration. The band-limiting spreads the 1 sample pulse to about 5 samples and produces “skirts” on the waveform. I want to emphasize that this file is emulating M-Noise. I am certain that the fine details are different from the real thing, but the concept is valid.
Wave 2 – M-Noise emulated to emphasize pulses
Below is a track that plays each wavelet used by CTA-2034. The standard requires a separate test for each of them to measure the maximum peak SPL based and the harmonic distortion limits. As with the pulses, I had to mix in some noise for the browser to play it, since very short duration events are interpreted as artifacts.
Wave 3 – Wavelets used for CTA-2034 peak testing
The Peak Events Contrasted
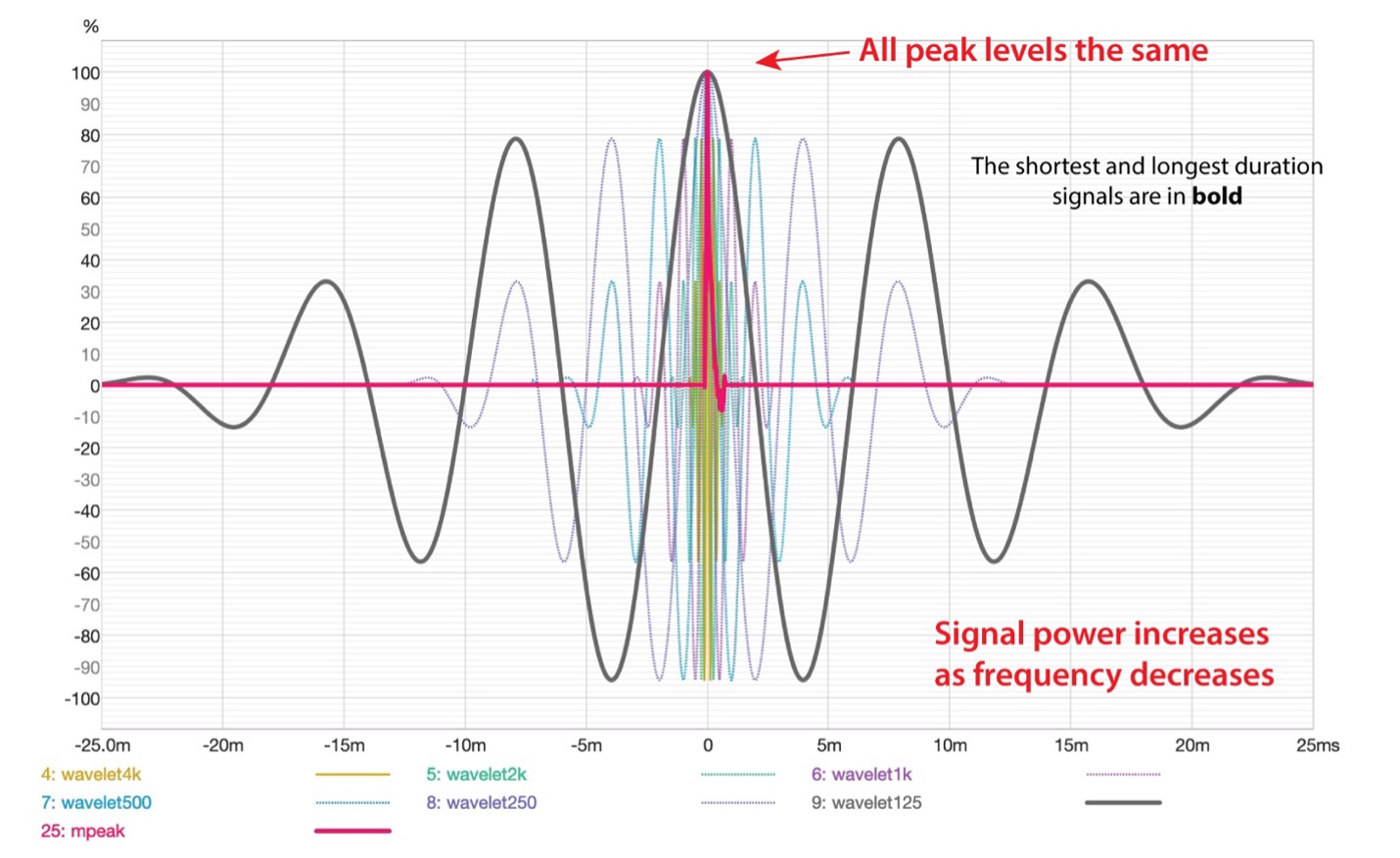
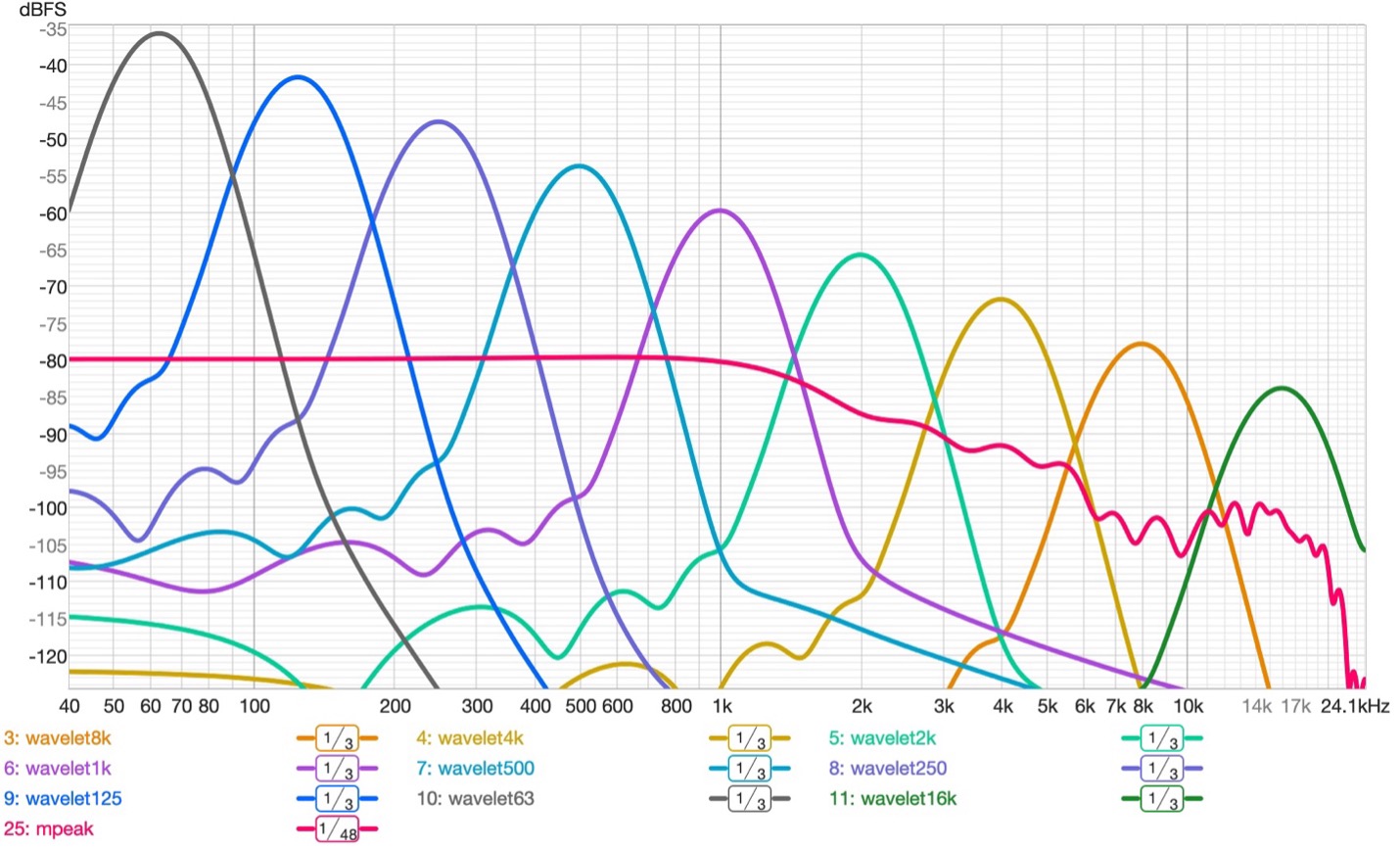
The waveform length and power spectrum of the wavelets and M-Noise pulse are shown in figures 7 and 8. Note that the wavelets are narrow band (1/3-octave). The M-Noise peak is broadband due to its short duration. It’s a high amplitude signal with very low signal power.
Figure 7 – The overlaid time domain waveforms of each stimulus, normalized to time zero. This proves that all have the same amplitude (0 dBFS).
Figure 8 – The signal power is proportional to the waveform length. The M-Noise peak (red) is broadband due to its short duration, but it has lower signal power than any of the wavelets for the same reason. Since its amplitude is 0 dBFS it produces a very high reading on a professional grade sound level meter that is fast enough to capture it.
In AES75 the embedded pulses are measured with a peak meter once the loudspeaker reaches its thermal limits (Figure 9). The M-Noise stimulus is required. The pulse peaks are typically 18 dB higher than the RMS voltage if the amplifier can pass them. This is why a very large amplifier is required. If the peaks are clipped (likely for an internally-powered loudspeaker) the transfer function is unaffected since the M-Noise peaks contain very little energy. This is why my measurements of the powered loudspeakers using IEC Noise and M-Noise produced the same continuous SPL even though the M-Noise signal was severely clipped.
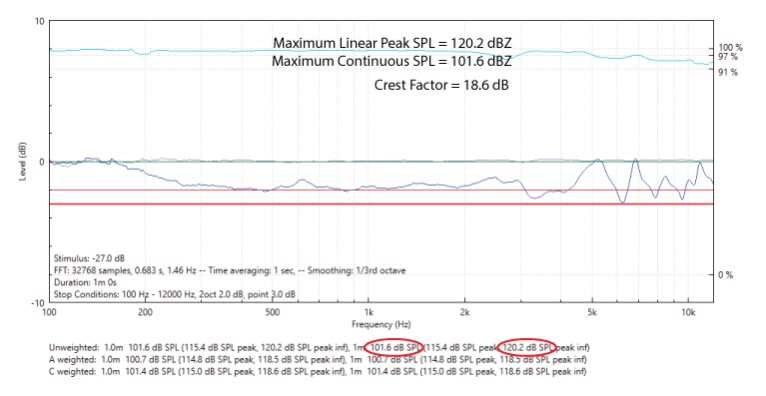 Figure 9– SpeakerMeasureTM screen at end of AES75 test. The maximum peak SPL is measured, but the peaks are not analyzed for distortion.
Figure 9– SpeakerMeasureTM screen at end of AES75 test. The maximum peak SPL is measured, but the peaks are not analyzed for distortion.
“Music-Likeness”
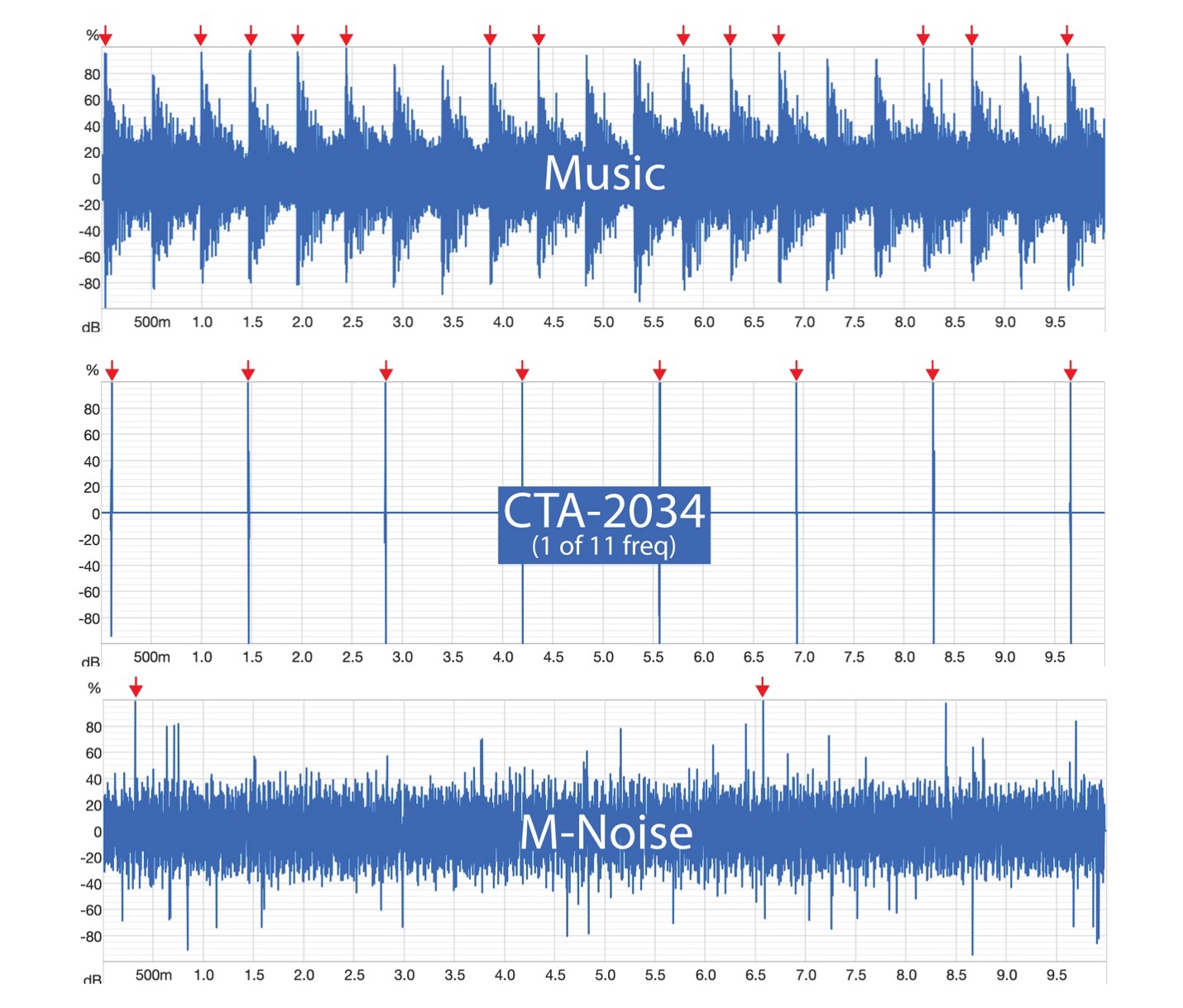
Both standards claim that the test signals are “music-like.” Figure 10 shows a 10-second span of heavily percussive music compared with the waveforms used by each standard to determine the maximum linear peak SPL.
Figure 10 – The red arrows show the number of full-scale events that occur in 10 s of program. These are the events that produce the maximum peak SPL. The music example is full-range with 18 dB crest factor. The wavelets are 1 kHz.
Music isn’t noise because it contains information. Information is produced by an intelligence. Music has order, cadence, pitch, repetition and structure. Any signal attempting to emulate it must have the same. Of the three waveforms in Figure 10, two contain information and one doesn’t.
Clearly there is a fundamental difference between the two standards regarding the definition of a meaningful signal peak. This is the fundamental reason why the maximum linear peak SPLs reported by the two standards are quite different.
Enough Theory – Here’s Some Data
The best way to compare the standards is to measure each on a line-up of loudspeakers. I chose a variety of loudspeaker types. They are as follows:
1. Cube – Passive: This is a 5-in transducer in a sealed box, driven by an amplifier meeting the AES75 specification (A Crown Studio Reference in bridged-mono mode).
2. Cube – Powered: This is an internally-powered version of the previous loudspeaker. The amplifier is much smaller.
3. 10H – Passive: A two-way 10-in with horn public address loudspeaker with internal passive crossover, driven by the reference amplifier.
4. Coax12 – Powered: A two-way public address loudspeaker that can be used for mains or monitors. It has internal processing and amplifiers.
5. Line Box – Powered: A two-way internally powered and processed line array box with two 10-in loudspeakers and line array high frequency element.
The test results are presented in Figure 11. The supporting data is presented in the appendix.
Figure 11 – The results of five loudspeakers tested to each standard.
Summary
I’ve presented the results on an investigation of how to measure the maximum linear peak SPL of a loudspeaker. For decades I’ve done it using D. B. Keele Jr’s wavelet method. This method was standardized by the Consumer Technology Association in 2015 as CTA-2034-A. The standard describes how to measure the “maximum output capability” of a loudspeaker using a single number rating produced from measuring the maximum continuous and maximum peak SPL.
In this article I described the peak SPL determination according to CTA-2034, and I am an advocate of using it as a stand-alone rating. After comparing it to the recently released AES75 standard, here are some thoughts and observations.
– Comparing the maximum linear peak SPL presented by the standards is like comparing apples and oranges.
– A sound system designer can expect to achieve an accurate maximum continuous SPL using the MIV produced by either standard. The M-Noise stimulus used by AES75 produces the approximate same continuous SPL and MIV as other noise types (e.g. IEC 60268-1 and CTA-2034).
– A sound system designer can expect to achieve the maximum linear peak SPL as reported by CTA-2034.
– The maximum linear peak SPL as given by AES75 will never be achieved in the real world. This is because for passive loudspeakers an unrealistically large amplifier is required to produce it from a very short pulse. When real-world limitations are considered, it’s a fictional rating.
– For some loudspeakers, the maximum continuous SPL and the maximum peak SPL are not all that different if a robust signal is used to determine the peak SPL and the signal is analyzed for distortion. The sound system designer is free to use either for amplifier selection, based on the intended application.
– I personally don’t think it’s a good idea to drive a loudspeaker with the largest possible audio amplifier to produce a rating. I also don’t think it’s a good idea to drive an internally powered loudspeaker with a noise signal that will be severely clipped when the thermal limit is reached.
Why It Matters
The biggest danger is that the uninformed may think that the maximum linear peak SPL as given by AES75 is meaningful. It’s a big number, and therefore the one that people will focus on. Both buyers and sellers like big numbers.
A manufacturer can quote this artificially high rating to sell a product and cite a professional standard as its source.
A contractor or consultant may choose a loudspeaker for its high maximum peak SPL, with little chance that it will be achieved under actual use since the voltage required to reproduce the peak is not given.
It is my hope that this investigation contributes to the discussion of meaningful loudspeaker maximum ratings. pb
Appendix (Click graphics to enlarge)
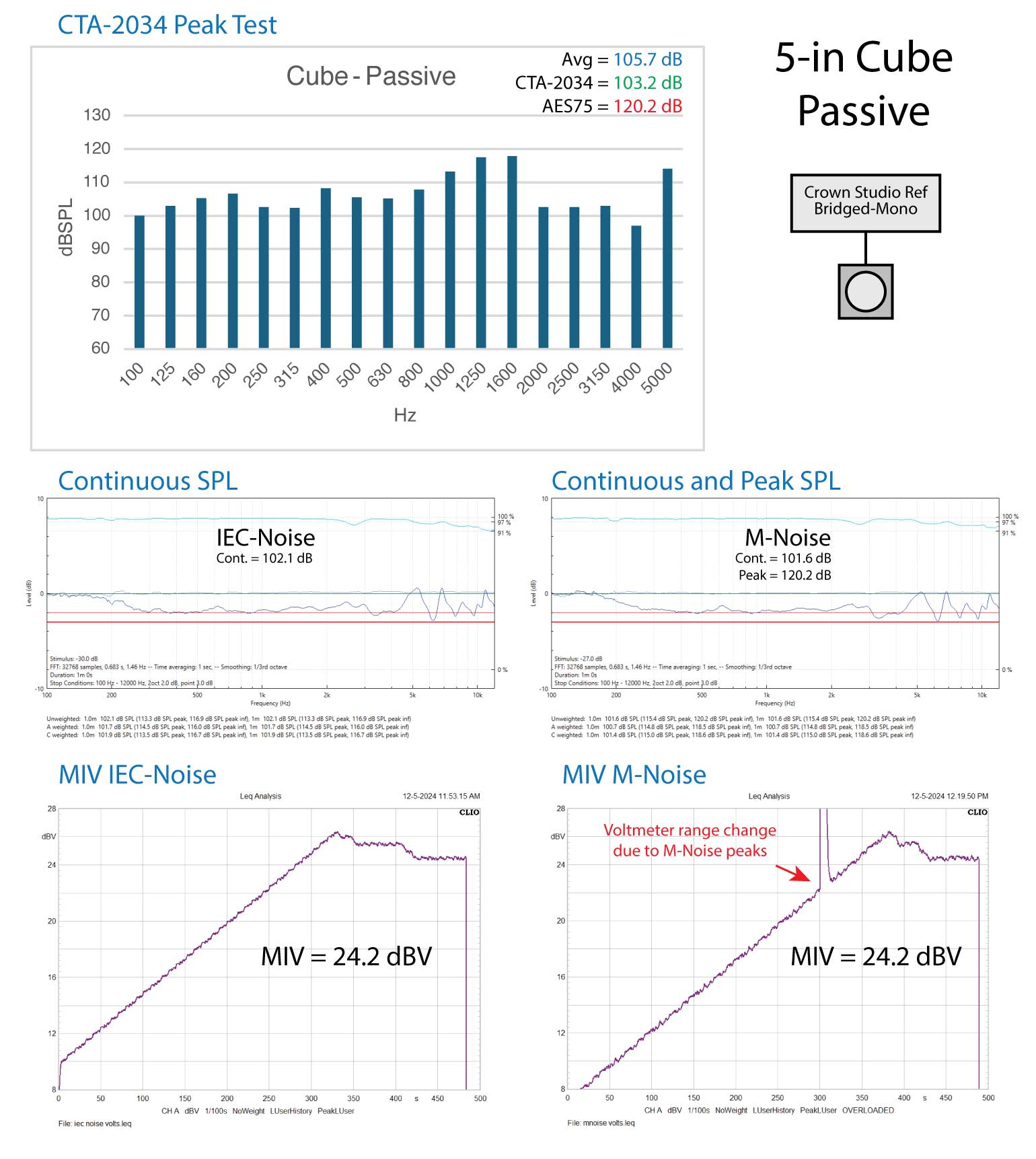 Figure 1A – Device 1 test results (above) (return)
Figure 1A – Device 1 test results (above) (return)
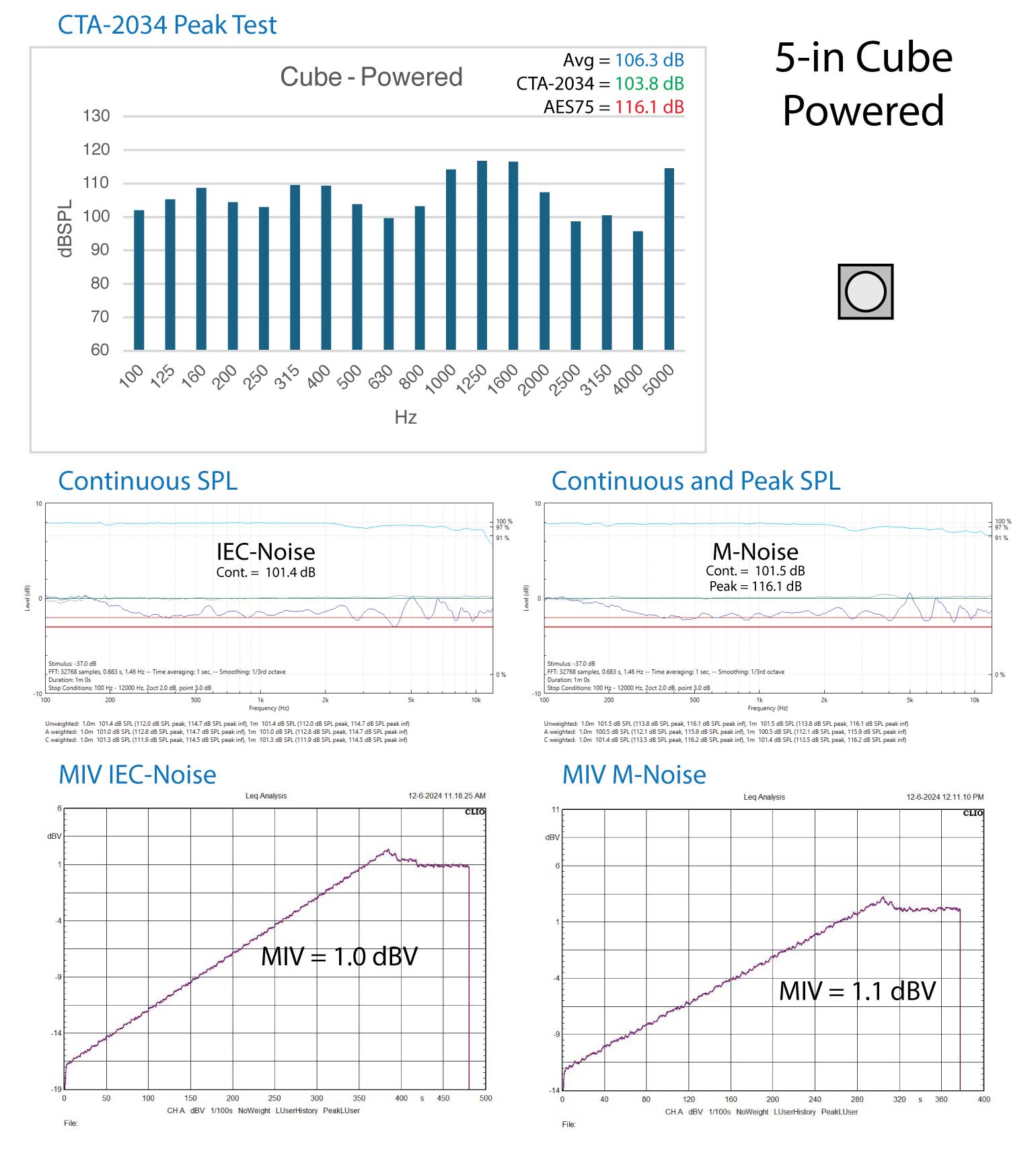 Figure 2A – Device 2 test results (above) (return)
Figure 2A – Device 2 test results (above) (return)
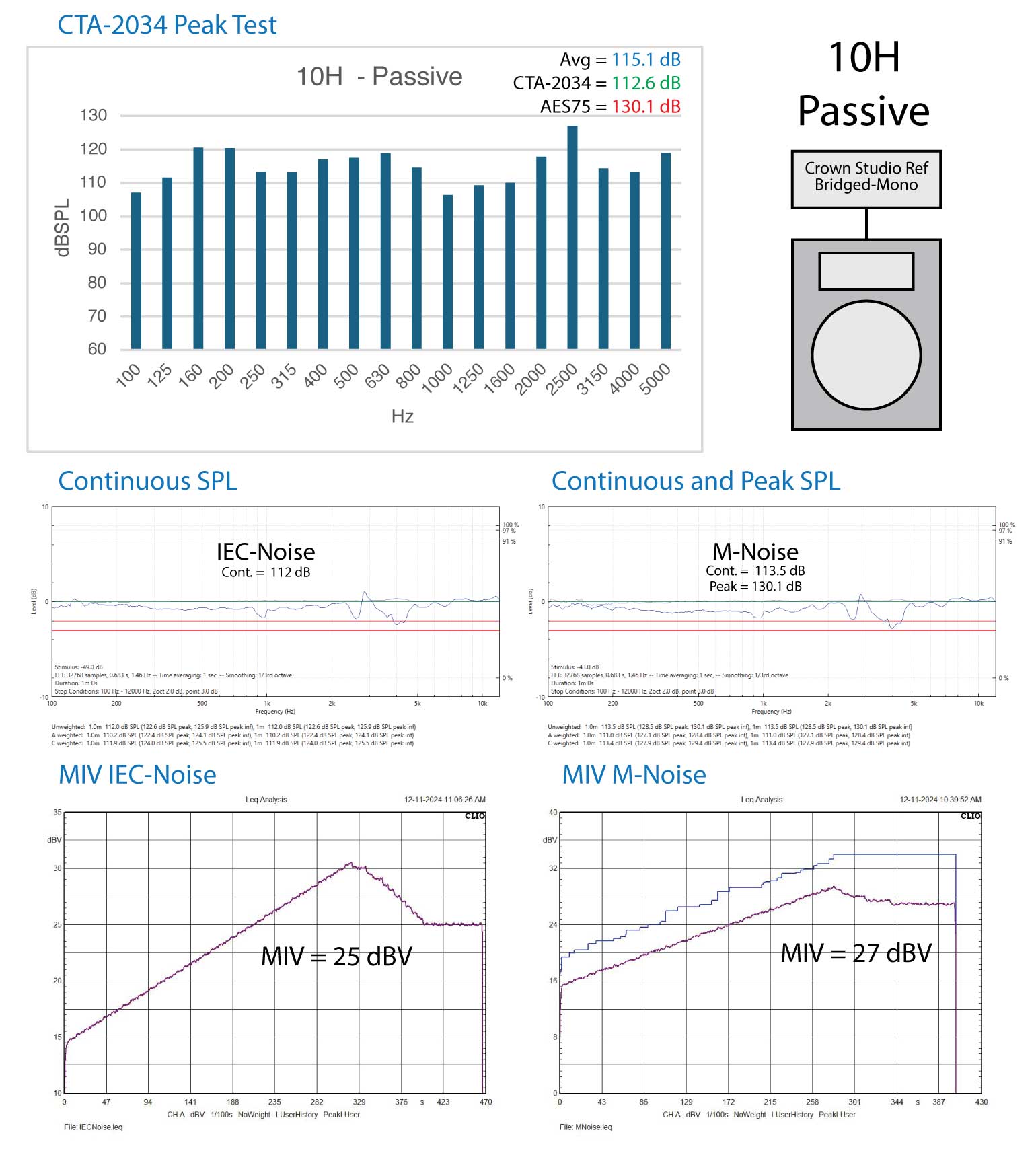 Figure 3A – Device 3 test results (above) (return)
Figure 3A – Device 3 test results (above) (return)
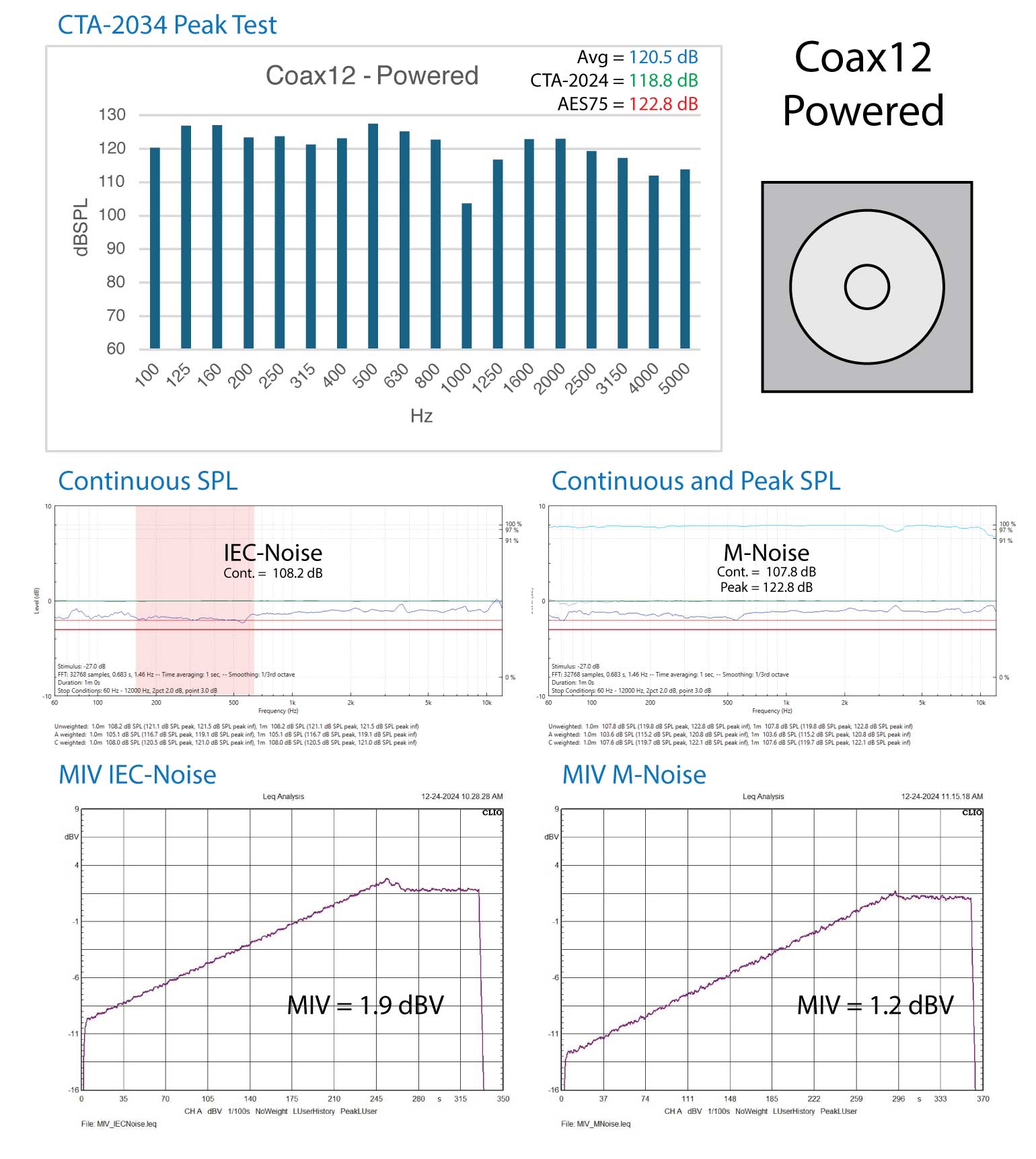 Figure 4A – Device 4 test results (above) (return)
Figure 4A – Device 4 test results (above) (return)
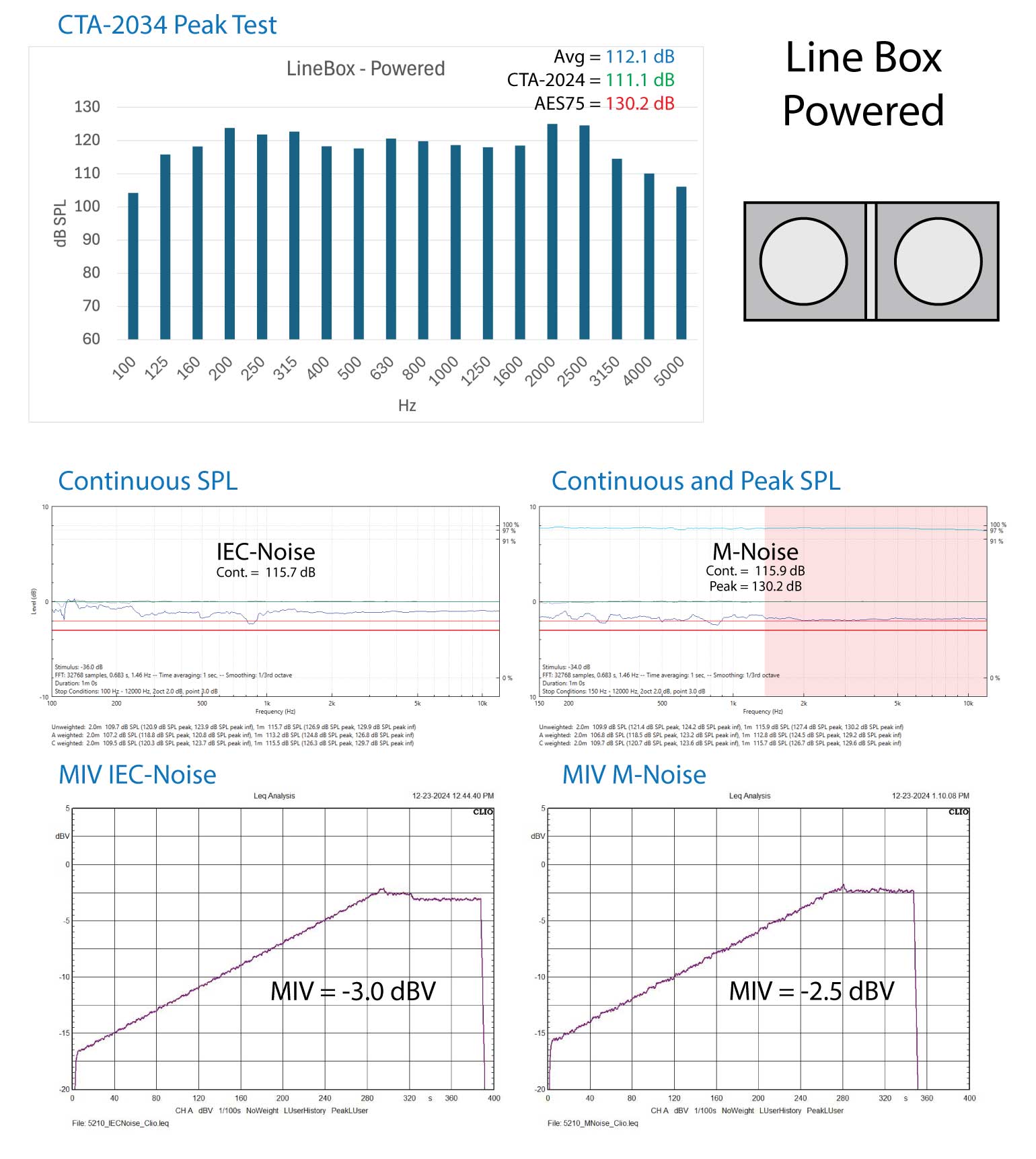 Figure 5A – Device 5 test results (above) (return)
Figure 5A – Device 5 test results (above) (return)