Is "CD Quality" Good Enough?

by Pat Brown

Is “CD Quality” Good Enough? In this article, Pat give you an opportunity to compare between 16 to 24 bit.

Flashback to earlier this spring when I started a discussion thread on the SAC Forum regarding digital audio resolution, citing a study that suggested that CD quality was sufficient to fully capture the frequency response and dynamic range detectable by humans. A fire storm ensued, and I posted that we would conjure up a digital resolution demonstration for the then upcoming SynAudCon Digital seminar, to be held in North Haven, CT. The seminar has come and gone, and we did indeed conduct the demo. Following is what we did, including some resources for replicating it on your own.

I will start by saying that this is a surprisingly controversial topic. Many audio practitioners are insulted by the suggestion that “CD quality” is good enough for their golden ears. We’re pros, right? We should be able to hear the difference between Switchcraft and Neutrik connectors, and we definitely deserve better than “CD Quality.”  In reality, CD quality may not be as bad as you think. Digital technology has long had sufficient bandwidth and dynamic range to satisfy human hearing (Figure 1). Is anything gained by making it better than it needs to be?

Figure 1 – This graphic compares some common digital resolutions. These are theoretical values. The green box highlights the approximate limits of human perception. The dashed red lines indicate the practical limits of current analog performance.

CD Quality

“CD quality” audio resolution uses a 16 bit word for each sample. The sample rate is 44.1 kHz. This is often described as simply “16/44.1k.” This translates into an analog dynamic range of approximately 96 dB, and an analog bandwidth of approximately 22 kHz. Technology broke through these limits long ago, and today the most common bit depth is 24 bits, and sample rates of 192 kHz and beyond are possible (24/192k). Those who deal with professional sound systems rarely encounter 44.1 kHz as a sample rate option. It has been increased to a more logical 48 kHz rate, yielding a bit more high frequency extension. Most DSPs use a 48 kHz sample rate and 24 bit words (24/48k).

The Price of Excess Resolution

Just because something is possible doesn’t mean it is necessary. Increasing the digital audio resolution beyond what is needed can strain playback and recording systems and force compromises that include lower channel counts, more storage space, a heavier processing load for your DSP, and greater required bandwidth for streaming. Higher bandwidth systems may be able to pass the “nasties” that often exist above 20 kHz, such as artifacts from switch-mode power amplifiers and noise shaping circuits. It’s entirely possible that these artifacts will be far higher in level than the harmonic content of the program material that you are trying to reproduce.

We want our bandwidth to be wide enough, but not too wide. At some point, “more” is not necessarily “better,” and in some cases it may be worse.

Digital Audio Resolution Demonstration

Theories and opinions abound on the Internet. As with most things, you can forget going there to get to the truth. The truth, in this case, is what is right for you. Digital resolution is something that you can self-assess, and I have created some resources that can help.

I decided to use the SAC Digital seminar for a resolution experiment. What better scenario than a room full of audio professionals, and three days of training on the fundamentals of digital audio? The idea was to configure a high resolution (24/192k) playback system that seminar attendees could use to compare digital resolutions. It immediately became apparent that 96 kHz of analog bandwidth all the way to the listener is an impossibility. Loudspeaker technology is limited to about half that, to be charitable, and air absorption would wreak havoc on anything higher than 20 kHz, even at a few meters. I dropped my target resolution to 24/96k and proceeded. My first stab at the playback system involved a custom two-way studio monitor with a ribbon tweeter. A 24/96k plate amplifier with on-board DSP was used to drive the monitor. I loaded the box, configured the plate amp, and measured the result. Once equalized the monitor was flat to about 40 kHz, which is very near the high frequency limit of my very expensive reference measurement microphone. This makes one ponder the HF limits of most studio and performance mics, but that’s a different topic. The system was minimum phase with the exception of the expected shift produced by low order IIR crossover network. I added a subwoofer to extend the low frequency bandwidth.

 

Coming up with a signal source was not nearly so easy. While many audio interfaces support up to 24/192 resolution for recording, none of them had analog or digital outputs that exceeded 90 dB of dynamic range and 20 kHz of bandwidth, which is not even CD quality. That’s not to say that they don’t exist, but I didn’t have carte blanche on the budget and wanted to use something I already owned. Every attempt to string several components together to form a system resulted in bandwidth compromises that invalidated the demo. And there in as a very important point – we need a system response that is better than CD quality, and I couldn’t come up with a way to get it (Photo 1).

Sennheiser to the Rescue

The digital seminar happened to be in North Haven, CT, which is very near Sennheiser’s US headquarters. They had some people registered for the class, and offered to help with demo equipment. As luck would have it, they happen to make a headphone playback system with resolution that exceeds the playback system that I was trying to assemble piece meal. Their HD 800 headphones, driven by the HDVD 800 digital headphone amplifier, is about as good as audio can get (Photo 2). It includes USB input with special drivers that support 24/192 playback. I would playback directly from a PC, eliminating all of the bottlenecks that I had been fighting in my previous attempts to assemble a high resolution system.

 

The bandwidth of the headphone system is

6 Hz – 51 kHz (-10 dB)

14 Hz – 44.1 kHz (- 3 dB)

This is probably the practical limit for any playback system, and you can knock some off of each end for even a wide bandwidth sound reinforcement system (24 Hz – 16 kHz).

So, I scrapped my 3-way studio monitor system and went with the headphone playback system. I re-learned a few lessons regarding the limitations of playback systems, mainly that adding another octave or two of high frequency extension is NOT trivial, and without it there may be no need for sample rates that exceed CD quality.

Photo 2 – The Sennheiser HD800 headphone listening system. This is the simplest possible signal chain for experiencing high resolution digital audio. If it is not audible on this system, it is not likely to be audible on any system.

Photo 3 – A SAC Digital attendee listens to the demo, as others await their turn.

The Program Material

The number of possible program sources exceeds infinity. I decided to create a “waveform olympics” track that each attendee could listen to through the system (Figure 2). The track would allow the evaluation of their high frequency hearing acuity and mid-band dynamic range. I also included some high resolution recording bites so that the demo wasn’t just test tones. I created the demo track in Adobe Audition, a professional-quality WAV editor. The resolution selected was 24/96k, because one simply cannot find or make recordings with frequency content higher than about 40 kHz, and playback is an even greater challenge. I know that marketing forces have led us to believe otherwise, but try it (measured results, please). I also theorized that if one couldn’t clearly hear the benefits of a 96 kHz sample rate, there was no point in doubling again to 192 kHz, which is an experiment we could revisit at the fall SynAudCon Digital seminar in Phoenix.

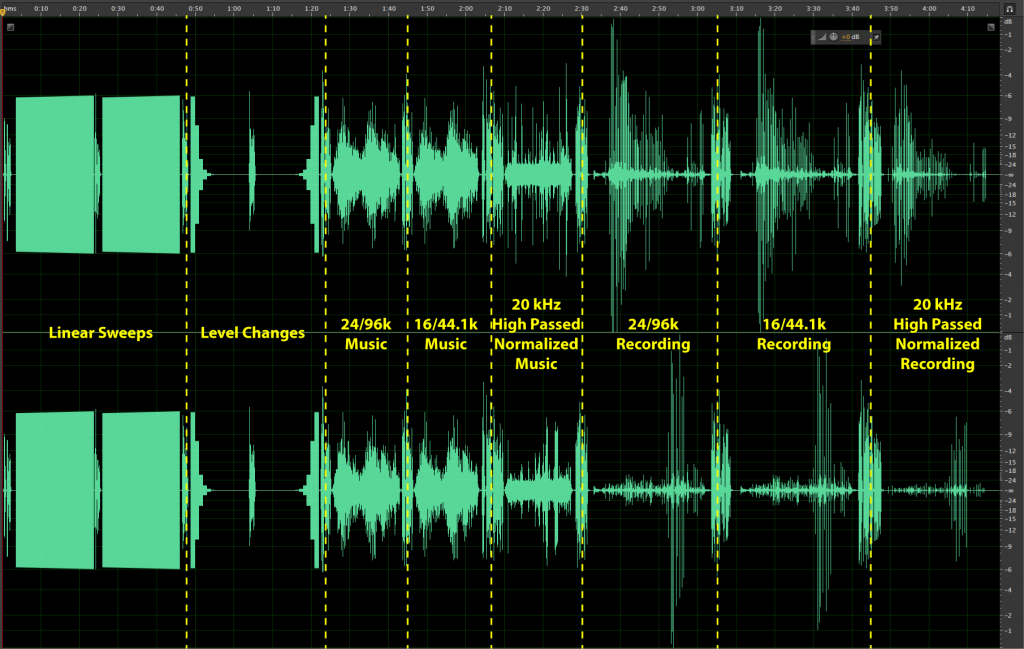
I first planned to use an Audio Precision analyzer (spectrum analyzer mode) to monitor the output of the headphone amplifier. This would prove the frequency response and dynamic range of the system. When set for the required resolution, the responsiveness of the display was less than stellar for monitoring program material. I opted instead to use the spectrum analyzer built into Adobe Audition. It tracked nearly perfectly with the program material, and allowed a linear display that makes the high frequency content clearly visible (Figure 2). The track includes the following:

• 1. Linear sine sweep from 20 Hz – 48 kHz. I used a linear sweep because it dwells much longer in the high frequency octaves than a log sweep. The listener judges at what frequency the tone disappears.
• 2. Linear sine sweep from 48 kHz – 20 Hz. The listener judges at what frequency the tone reappears.
• 3. Multi-tone fade out for evaluating dynamic range. I picked a series of frequencies in the upper mid-range where human hearing is most sensitive. The tones start at -6 dB full-scale, and fade incrementally into the noise floor. I ended up reducing the initial levels by 10 dB for the live demo because they were deafening and rather startling to the listeners. I left them intact in the download file, so keep that in mind. The level drops are incremental, starting at 10 dB/step at the higher levels and reducing to 5 dB/step at the lower levels. This was necessary to achieve a controlled level reduction that can be judged by looking at the level meters of your wave editor. The noise floor of the Sennheiser playback system was inaudible, so the tones did not fade into noise – rather they faded to inaudibility.
• 4. Multi-tone fade in. This is the reverse of the previous track, which allows the listener to judge the lowest level at which they can hear the tones appear rather than disappear. The levels are visible on the vertical axis of the spectrum analyzer, allowing the listener to judge a “dB re. full-scale” level at which they could no longer hear the tones.
• 5. High resolution music segment (24/96k) with violins with strong harmonic content above 20 kHz.
• 6. The same segment, but resampled to CD quality (16/44.1k).
• 7. The same segment, but with the spectral content below 20 kHz eliminated with a brick-wall filter, leaving only the spectral content above 20 kHz. When spectral content beyond 20 kHz does exist on a recording, it is usually very low in level. I normalized this to full-scale, which adds about 30 dB of gain. This greatly increases the likelihood of audibility.
• 8. A recording of scissors cutting hair, with strong spectral content above 20 kHz. I processed it in the same ways as the previous track, which yielded the “just better than CD quality” version, as well as the track that only includes the above 20 kHz content, normalized to full scale.

You can download the track for your own experimentation at the end of this article. Keep in mind that you will need a stellar playback system to get the full effect, and the louder you play it, the more dynamic range will be audible. The sample rate of your sound card should be 96 kHz. It probably isn’t now.

Figure 2- The “Waveform Olympics” audio track, with annotations describing each segment.

“Waveform Olympics” – The Movie

The following video is a screen capture of the demonstration. It adds some visual relevance to the explanation. This is Adobe Audition’s “Frequency Analysis” window and “Peak Level Meter” window, placed side-by-side. The frequency (horizontal) axis is linear. This more clearly displays the frequency range that would be missing on a CD, or alternately, be included using a 96 kHz sample rate. I have marked the “CD quality” limits for both frequency and dynamic range. Here is a link to the MOV movie file (~300 MB).

Wave_Olympics_v(1,0)

 

Figure 3 – A frame from the “Waveform Olympics” movie. The limits of CD quality are indicated. Any aspect of the waveform beyond these boundaries would not be preserved at 16/44.1k.

Conclusion

The objective of the experiment was to give each attendee the opportunity to form their own opinion as to the required digital resolution for satisfying the needs of their hearing. It was not a scientific experiment or double-blind A-B test, conducted to publish the results or prove a point. Plenty of those have been done, and the results and conclusions are always a source of contention, doubt, angry blog posts and shouting matches. What is important is for an individual to determine what they believe, by actual experience, rather than from reading the scores of opinions published on the internet. This will profoundly affect your philosophy regarding digital audio, and influence the systems that you design.

I’d be remiss if I didn’t share at least my own opinion, based on the demonstration described. It is as follows. Regarding sample rate, I don’t believe that spectral content above 20 kHz is audible to humans. Period. No one at the seminar claimed to hear the portions of the demo tracks designed to make it audible – under the most controlled conditions I could create. It is a valid argument that higher-than-48 kHz sampling may in some cases be required to produce an end result that is accurate at 20 kHz. But, this is due to poor converters, not the needs of the human auditory system.

Regarding bit depth, I believe that an honest 16 bits is sufficient to fully capture the dynamic range of the linear range of human hearing. The demo track revealed audibility to about -80 dBFS, to be charitable, which equates to about 13 bits. This is from a starting SPL that bordered on uncomfortable, and was at or very near the maximum SPL possible from the playback system. Granted, if your playback system produces 130 dB-SPL then you may indeed be able to hear content that is down 100 dB in level, assuming you are in a room with a very low noise floor. Under these conditions, there could be a benefit from increasing the bit depth beyond 16 bits.

The fact that most converters use 24 bit resolution means that we can waste some of the possible dynamic range and still produce a result that is adequate for human hearing.

So, is “CD Quality” good enough? I’ll stick my neck out and state that properly utilized, it actually IS good enough for the delivery of program material to a human listener. Not only is it good enough, it is probably all that is possible given the many potential bottlenecks in real world playback chains. The fact that we can have higher resolution means that a “CD quality” end result may be achieved using sloppier recording techniques and a non-optimal system gain structure – and that’s a good thing.

The Fine Print

Some important caveats and clarifications follow..

• This discussion is about the analog resolution that results from 16/44.1k conversion. Cheap 16/44.1k codecs that do not realize this resolution abound. We used great gear for the demo. Yes, the room could have been quieter, but it wasn’t bad, and the use of headphones minimized the impact of the room’s noise floor.
• I don’t dispute that there are some benefits of using higher sample rates beyond achieving higher playback resolution, such as lower latency in a DSP. It’s a valid argument that it is better to have too much resolution than not enough, just as with pixels in a digital photo. I could agree with using a 96 kHz sample rate for the recording and production processes, where the intent is to end up at CD quality after processing, etc. At least the increased bandwidth will be measurable, if not audible.
• I don’t dispute that people hear differences between digital devices. This usually gets attributed to resolution, because that is the easiest thing to blame. The actual cause (and there can be many) is usually unknown.
• It’s great to have a playback system that exceeds the performance level needed. The Sennheiser system we used for the demo was coveted by all, including me, and it is worth every dime of its $3500 price tag. For me it is not because it supports 24/192k resolution, but because it is robust in design and construction and has versatile I/O, including analog. If I owned it, I would run it at 24/48k.
• In professional sound system work, the 44.1 kHz sample rate has been replaced by 48 kHz, making 24/48k digital audio a standard of sorts, and the highest resolution needed for full-bandwidth audio reproduction. From the listening demo, even a 32 kHz sample rate (16 kHz audio bandwidth) would have been sufficient for most listeners, including myself.
• “CD quality” performance would be quite an accomplishment for a sound reinforcement system. I doubt that there is a “large room” system in existence that realizes 96 dB of dynamic range and flat frequency response to 22 kHz. An IMAX theater probably comes the closest.
• A thought-provoking expose on digital resolution is available here. This is what sparked the Forum discussion to start with. While some flaws have been pointed out in the the author’s presentation, they are minor and don’t detract from his main points.

My opinion is just that – my opinion. But, it is based on an honest confrontation with the question, and many hours spent seeking an objective proof of the need for “more” that did not materialize in spite of my best efforts. To me, the real danger is those that have formed their opinion from the opinions of others, often based on unsubstantiated claims and anecdotal evidence. There are already those that would brand a DSP operating at 48 kHz as “insufficient” or “low fidelity.” This can ultimately bring marketing pressure on manufacturers to “drink the cool-aid” and support the higher resolutions with the attendant performance trade-offs. Do I really want to double the amount of digital audio information (assuming 96 kHz vs. 48 kHz) to reproduce a frequency range that is not audible to humans? You should decide for yourself.  pb

 

Download the “Wave Olympics” wave file (150 MB)