What's a DLL – Line Array Predictions vs Measurement (Part 2)
Pat Brown examines line array predictions and how they compare to the actual measurements.
Introduction
Accurate coverage predictions are essential for determining an appropriate line array configuration for a venue. A hot item in the audio engineering marketplace is software for predicting the performance of line arrays. It’s always tempting to take information generated by a computer at face value, but it’s good science to compare the predicted responses with actual measurements.
A hindrance to such comparisons is the great difficulty in measuring balloon data for line arrays. Their large size makes them unwieldy to rotate with accuracy, and their response is distance-dependent in their near-field. So even if you go to the trouble to measure one, the data collected at a specific distance is only accurate for that distance. In addition, some line arrays use signal processing to shape the balloon and steer the array, creating an almost infinite number of configurations. These factors make it impractical to use measured data alone for general prediction purposes, and make accurate line array predictions attractive to sound system designers.
A logical solution is to combine both methods – start with far-field measured data for a single line array element, and use predictions to determine the response of multiples at various distances. This is the approach that will be examined in this article.
Since this is a correlation study, we will create a scenario that falls within the bounds of our measurement setup – namely an 8 meter distance limitation for balloon measurements. If the correlation between the measurements and predictions is good, then we can move on to evaluating larger multiples and greater distances in future articles. The procedure is as follows:
- 1. Measure a single line array element.
- 2. Measure multiples of the same element. This yields hard data for the actual performance of the array.
- 3. Use the data from the single element in prediction software to predict the response of multiple elements.
- 4. Evaluate the correlation between the measured and predicted responses for the multiple element configurations.
Theory
The mathematics used to predict the interaction between array elements is mature. Excellent texts on this subject date back to early in the last century. Classical texts by Beranek, Olson and others lay the theoretical groundwork. Today’s technology adds speed of implementation, practicality and high resolution graphical displays.
The Device
The device chosen is designed to be a line array building block – meaning that sound radiation comes from the entire surface of the device, even at high frequencies. It shall remain nameless, but its measured response is given. The response is typical of any line array element of similar physical size (Figure 1). Since measured balloon data is used for this single element, good correlation between measured and predicted responses for multiples of this device would suggest that similar correlation can be expected for different devices, as long as accurate measured balloon data is available for the single array element. It is the process that is being examined, not the loudspeaker. The device is sufficiently small to allow three units to be measured at our limiting distance of 8m. Future studies at greater distances will force us to move outside of a controlled environment.
Some Important Points
Due to the almost infinite number of device types and possible configurations, it is not possible to test them all. Some general implications should be remembered:
- – Good correlation between measured and predicted at 8m gives confidence that predictions for greater distances will have similar accuracy.
- – Good correlation for 3 elements gives confidence that predictions made for larger numbers of elements will have similar accuracy.
- – Poor correlation for either in this relatively simple case reduces confidence in line array predictions in general.
Data Display
Once the data is collected, it must be displayed in a meaningful way that facilitates comparisons. The method chosen is to create a data file for the measured configurations using the Common Loudspeaker File Format (CLF). The stand-alone CLFViewer allows the data for the single element to be viewed without further investment on the part of the reader. The CLF data for the single device is then used in prediction software for simulations of multiple devices. The prediction software used is CATT-Acoustic™, specifically the ARRAY0 module (Figure 2). This is the same package that was used for Part 1 of this series. ARRAY0 provides a common denominator between the measurements and predictions because it can display the CLF data at its internal resolution, as well as use it to predict the polars and balloons of the various configurations. In addition, ARRAY0 allows the user to select the observation distance for the generation of the balloon data and polar data. This distance can be anywhere in the near-field or far-field of the array. This capability facilitates distance-specific studies and comparisons. ARRAY0 provides a virtual measurement environment that combines measured data with prediction. If sufficiently accurate, one can easily see its usefulness for designing and configuring line arrays, since the process can be streamlined by creation of a DLL.
Resolution 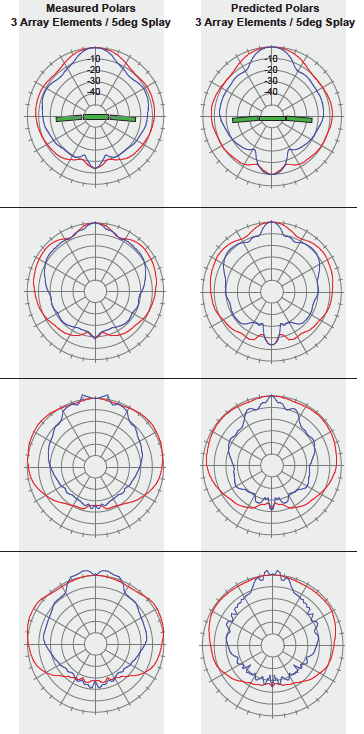
A meaningful frequency and angular resolution must be selected for both measured and predicted data. The measured data was made at 5- deg angular increments and 1/3-octave frequency resolution. These are practical and well-accepted resolutions for balloon data within the audio industry.
In the same way that an appropriate resolution must be selected for the measured data, both angular and frequency resolution must be selected for the predicted data. The ARRAY0 module can use any angular resolution internally. For plotting the resolution is 2-deg for polars and 5-deg for balloons. Frequency resolutions supported are 1/1-octave, 1/3-octave and 1/6-octave. The 1/1-octave resolution uses only the center frequency of the octave band. This is not recommended as it presents how the array might perform with a sinusoidal input. Lobing will be over-emphasized and coverage will not be modeled well. 1/6-octave is the default and recommended resolution. The 1/6-octave values are averaged and displayed at 1/1-octave center frequencies.
The full-range performance of each configuration was measured and predicted. Due to space constraints the 1kHz, 2kHz, 4kHz, and 8kHz octave bands are presented in this article. Since the potential for inaccuracy in predictions increases with frequency, the 8kHz octave band is of particular interest. For several reasons, it is the highest octave band at which coverage can be expected to predict with reasonable accuracy. Some of these reasons include:
- 1. The difficulty in measuring the far-field response of the single array element at higher frequencies due to distance constraints in the measurement setup. It is essential that far-field data be measured for the single device. The larger the device, the further away you must be. Failure to observe this invalidates all predictions made with the data for frequencies for which the far-field criteria are not met.
- 2. The adverse effects of temperature gradients and humidity on the measured data increase with frequency.
- 3. The effects of reflections from cabinet edges and diffraction increase with frequency and make the response of the array element increasingly dependent on its location in the array (also true for low frequencies).
The resultant correlation between measured and predicted data can indicate at what frequencies the above factors are becoming significant.
Okay, Let’s Compare
The plots on the preceding pages show the comparison between the measured and predicted data. I chose simple polars to save space. For line arrays it is the vertical polar that is of the greatest interest, since shaping it is the whole point of using a line array. There’s a lot of data, and the plots are small. The on-line PDF version of this article is high resolution and allows the plots to be greatly magnified for closer observation.
The main vertical lobe of the arrays (blue curve aimed toward top of page) predicted well for the 1kHz and 2kHz octave bands. The correlation is quite good with the predictions giving an almost identical coverage angle as the measured configurations.
At 4kHz and 8kHz it is clear that the measured coverage angle is much wider than the predicted coverage angle for the 5-degree splay configuration (Figure 3). This warrants further investigation, because it demonstrates a potential disconnect between predictions and actual performance.
The lower correlation at 8kHz is troublesome. We know that the measured data is correct, and from the lower octave bands we know that the prediction method is accurate and can potentially give the correct result. Since the single element is several wavelengths high at these octave bands, it cannot be assumed to be a point source. The problem lies not with the prediction software, nor with the measured data, but in how we model the single element at high frequencies.
The next article in this series will focus on the factors that can reduce the correlation between line array predictions and actual performance, and offer some possible solutions for improving the high frequency accuracy of array predictions.
The implications are clear. We’ve shown that accurate line array predictions are possible given good data input and prediction algorithms. This gives the sound system designer an indispensable tool – the ability to accurately check array coverage at the drawing board stage of a project. pb



